题目内容
【题目】为了解决“经过平面上的100个点中的任意两点最多能画出多少条直线”这个问题,数学课外兴趣小组的同学们讨论得出如下方法:当![]() 时,画出最多直线的条数分别是:
时,画出最多直线的条数分别是:
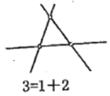
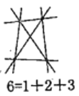
过两点画一条直线,三点在原来的基础上增加一个点,它与原来两点分别画一条直线,即增加两条直线,以此类推,平面上的10个点最多能画出![]() 条直线.
条直线.
请你比照上述方法,解决下列问题:(要求作图分析)
(1)平面上的20条直线最多有多少个交点?
(2)平面上的100条直线最多可以把平面分成多少个部分?平面上![]() 条直线最多可以把平面分成多少个部分?
条直线最多可以把平面分成多少个部分?
【答案】(1)20条直线最多有1+2+3+…+19=190个交点;(2)5051部分,![]() 部分
部分
【解析】
(1)根据题意当有2,3,4条直线时,作图可得到最多交点的个数,找到规律即可得到20条直线可得到最多交点的个数;
(2)根据题意当有1,2,3条直线时,作图可得到最多可把平面分成的部分个数,找到规律即可得到100条直线最多可以把平面分成的部分个数,进而找到平面上![]() 条直线最多可以把平面平面分成的部分个数.
条直线最多可以把平面平面分成的部分个数.
解:(1)如图,当有2,3,4条直线时最多交点的个数分别是:1,3,6
∵1=1,
3=1+2,
6=1+2+3,
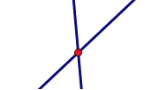
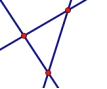
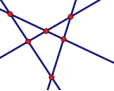
∴20条直线最多有1+2+3+…+19=190个交点;
(2)当有1,2,3条直线时最多可把平面分成的部分分别是:2,4,7
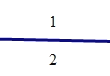
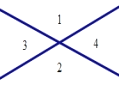
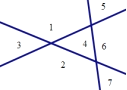
∵2 =1+1
4=1+(1+2)
7=1+(1+2+3)
∴100条直线最多可把平面分成
1+(1+2+3+…+100)=5051个部分
同理n条直线最多可把平面分成
1+(1+2+3+…+n)=![]() .
.

【题目】某班进行了一次数学測验,将成绩绘制成频数分布表和频数直方图的一部分如下:
成绩 | 频数(人数) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
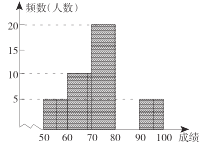
(1)在频数分布表中,![]() 的值为________,
的值为________,![]() 的值为________;
的值为________;
(2)将频数直方图补充完整;
(3)成绩在![]() 分以上(含
分以上(含![]() )的学生人数占全班总人数的百分比是多少?
)的学生人数占全班总人数的百分比是多少?
【题目】如图,边长为 7 的正方形 OABC 放置在平面直角坐标系中,动点 P 从点 C 出发,以 每秒 1 个单位的速度向 O 运动,点 Q 从点 O 同时出发,以每秒 1 个单位的速度向点 A 运动,到达端点即停止运动,运动时间为 t 秒,连 PQ、BP、BQ.
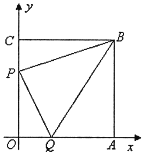
(1)写出 B 点的坐标;
(2)填写下表:
时间 t(单位:秒) | 1 | 2 | 3 | 4 | 5 | 6 |
OP 的长度 | ||||||
OQ 的长度 | ||||||
PQ 的长度 | ||||||
四边形 OPBQ 的面积 |
①根据你所填数据,请描述线段 PQ 的长度的变化规律?并猜测 PQ 长度的最小值.
②根据你所填数据,请问四边形 OPBQ 的面积是否会发生变化?并证明你的论断;
(3)设点 M、N 分别是 BP、BQ 的中点,写出点 M,N 的坐标,是否存在经过 M, N 两点的反比例函数?如果存在,求出 t 的值;如果不存在,说明理由.