题目内容
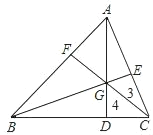
【题目】如图所示,△ABC中,点D、E、F分别在三边上,E是AC的中点,AD、BE、CF交于一点G,BD=2DC,S△GEC=3,S△GDC=4,则△ABC的面积是( )

A.25B..30C.35D.40
【答案】B
【解析】
由于BD=2DC,那么结合三角形面积公式可得S△ABD=2S△ACD,而S△ABC=S△ABD+S△ACD,可得出S△ABC=3S△ACD,而E是AC中点,故有S△AGE=S△CGE,于是可求S△ACD,从而易求S△ABC.
.解:BD=2DC,
∴S△ABD=2S△ACD,
∴S△ABC=3S△ACD,
∵E是AC的中点,
∴S△AGE=S△CGE,
又∵S△GEC=3,S△GDC=4,
∴S△ACD=S△AGE+S△CGE+S△CGD=3+3+4=10,
∴S△ABC=3S△ACD=3×10=30.
故选:B.

练习册系列答案
相关题目