题目内容
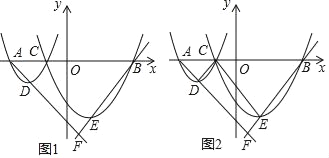
【题目】如图1，在平面直角坐标系xOy中，已知A、B两点的坐标分别为（﹣4，0）、（4，0），C（m，0）是线段AB上一动点（与A、B两点不重合），抛物线l1：y=ax2+b1x+c1（a＞0）经过点A、C，顶点为D，抛物线l2：y=ax2+b2x+c2（a＞0）经过点C、B，顶点为E，直线AD、BE相交于F．
（1）若a=
，m=﹣1，求抛物线l1、l2的解析式；
（2）若a=1，∠AFB=90°，求m的值；
（3）如图2，连接DC、EC，记△DAC的面积为S1，△ECB的面积为S2，△FAB的面积为S，问是否存在点C使得2S1S2=aS，若存在，请求出C的坐标；若不存在，请说明理由．
【答案】（1）L1解析式为y=
x2+
x+2；L2解析式为y=x2﹣
x﹣2；（2）m=±2
；（3）C（2
，0）或（﹣2，0）.
【解析】
（1）利用待定系数法，将A，B，C的坐标代入解析式即可求得二次函数的解析式；
（2）过点D作DG⊥x轴于点G，过点E作EH⊥x轴于点H，易证△ADG～△EBH，根据相似三角形对应边比例相等即可解题；
（3）构建一次函数，利用方程组求出点F坐标，再根据2S1S2=aS，构建方程求出m即可解决问题；
解：（1）解：（1）将A、C点带入y=ax2+b1x+c1中，可得：
，解得：
，
∴抛物线L1解析式为y=x2+
+2；
同理可得：
，解得：
，
∴抛物线L2解析式为y=x2﹣x﹣2；
（2）如图，过点D作DG⊥x轴于点G，过点E作EH⊥x轴于点H，
由题意得：
，解得：
，
∴抛物线L1解析式为y=x2+（4﹣m）x﹣4m；
∴点D坐标为（
，﹣
），
∴DG=，AG=
；
同理可得：抛物线L2解析式为y=x2﹣（m+4）x+4m；
∴EH=
，BH=
，
∵AF⊥BF，DG⊥x轴，EH⊥x轴，
∴∠AFB=∠AGD=∠EHB=90°，
∵∠DAG+∠ADG=90°，∠DAG+∠EBH=90°，
∴∠ADG=∠EBH，
∵在△ADG和△EBH中，
，
∴△ADG～△EBH，
∴
，
∴
=
，化简得：m2=12，
解得：m=±2；
（3）设L1：y=a（x+4）（x﹣m）=ax2+（4﹣m）ax﹣4ma，L2：y=a（x﹣4）（x﹣m）=ax2﹣（4+m）ax+4ma，
∴D（，﹣
a），E（，﹣ a），
∴直线AF的解析式为y=﹣
x﹣2a（m+4），直线BF的解析式为y=﹣
x+2a（m﹣4），
由
，解得
，
∴F（﹣m，
），
∵2S1S2=aS，
∴2××（m+4）×a××（4﹣m）×=a××8×[﹣
a]，
整理得：（m2﹣16）2=64，
∴m2﹣16=±8，
解得m=±2或±2
（舍弃），
∴C（2，0）或（﹣2，0）；
