题目内容
【题目】如图,在平面直角坐标系中,O为坐标原点,直线l1:y=kx+4与y轴交于点A,与x轴交于点B.
(1)请直接写出点A的坐标:______;
(2)点P为线段AB上一点,且点P的横坐标为m,现将点P向左平移3个单位,再向下平移4个单位,得点P′在射线AB上.
①求k的值;
②若点M在y轴上,平面内有一点N,使四边形AMBN是菱形,请求出点N的坐标;
③将直线l1绕着点A顺时针旋转45°至直线l2,求直线l2的解析式.
【答案】(1)(0,4);(2)①k=![]() ;②N(-3,
;②N(-3,![]() );③直线l2的解析式为y=
);③直线l2的解析式为y=![]() x+4.
x+4.
【解析】
(1)令![]() ,求出相应的y值,即可得到A的坐标;
,求出相应的y值,即可得到A的坐标;
(2)①先设出P的坐标,然后通过点的平移规律得出平移后![]() 的坐标,然后将
的坐标,然后将![]() 代入
代入![]() 中即可求出k的值;
中即可求出k的值;
②作AB的中垂线与y轴交于M点,连结BM,分别作AM,BM的平行线,相交于点N,则四边形AMBN是菱形, 设M(0,t),然后利用勾股定理求出t的值,从而求出OM的长度,然后利用BN=AM求出BN的长度,即可得到N的坐标;
③先根据题意画出图形,过点B作BC⊥l1,交l2于点C,过点C作CD⊥x轴于D,利用等腰三角形的性质和AAS证明△AOB≌△BDC,得出AO=BD,OB=DC,进一步求出点C的坐标,然后利用待定系数法即可求出直线l2的解析式.
(1)∵y=kx+4与y轴交于点A,
令![]() ,
,![]() ,
,
∴A(0,4).
(2)①由题意得:P(m,km+4),
∵将点P向左平移3个单位,再向下平移4个单位,得点P′,
∴P′(m-3,km),
∵P′(m-3,km)在射线AB上,
∴k(m-3)+4=km,
解得:k=![]() .
.
②如图,作AB的中垂线与y轴交于M点,连结BM,过点B作AM的平行线,过点A作BM的平行线,两平行线相交于点N,则四边形AMBN是菱形.
![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,解得
,解得![]() ,
,
∴![]() .
.
设M(0,t),则AM=BM=4-t,

在Rt△BOM中,OB2+OM2=BM2,
即32+t2=(4-t)2,
解得:t=![]() ,
,
∴M(0,![]() ),
),
∴OM=![]() ,BN=AM=4-
,BN=AM=4-![]() =
=![]() ,
,
∴N(-3,![]() ).
).
③如图,过点B作BC⊥l1,交l2于点C,过点C作CD⊥x轴于D.则∠ABC=∠BDC=90°,
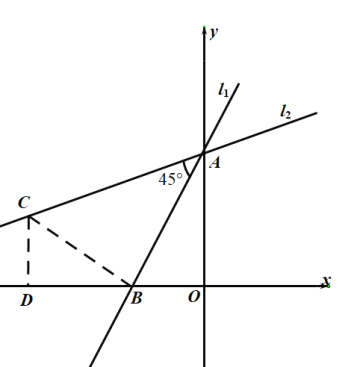
∵∠BAC=45°,
∴△ABC是等腰直角三角形,
∴AB=BC,∠ABO+∠CBD=90°,
又∵∠ABO+∠BAO=90°,
∴∠BAO=∠CBD,
在![]() 和
和![]() 中,
中,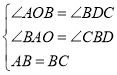
∴△AOB≌△BDC(AAS),
∴AO=BD=4,OB=DC=3,
∴OD=OB+BD=3+4=7,
∴C(-7,3),
设直线 l2的解析式为:y=ax+4,
则-7a+4=3,
解得:a=![]() .
.
∴直线 l2的解析式为:y=![]() x+4.
x+4.

 阅读快车系列答案
阅读快车系列答案