题目内容
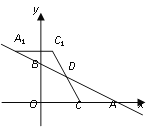
【题目】如图,一次函数y=-![]() x+m(m>0)的图像与x轴、y轴分别交于点A、B,点C在线段OA上,点C的横坐标为n,点D在线段AB上,且AD=2BD,将△ACD绕点D旋转180°后得到△A1C1D.
x+m(m>0)的图像与x轴、y轴分别交于点A、B,点C在线段OA上,点C的横坐标为n,点D在线段AB上,且AD=2BD,将△ACD绕点D旋转180°后得到△A1C1D.
(1)若点C1恰好落在y轴上,试求![]() 的值;
的值;
(2)当n=4时,若△A1C1D被y轴分得两部分图形的面积比为3:5,求该一次函数的解析式.
【答案】(1) ![]() ;(2)
;(2) ![]() 或
或![]()
【解析】试题分析:(1)由题意,得B(0,m),A(2m,0).过点D作x轴的垂线,交x轴于点E,交直线A1C1于点F,易求![]() 的值;
的值;
(2)由(1)得,当m>3时,点C1在y轴右侧;当2<m<3时,点C1在y轴左侧.分类讨论即可得解.
试题解析:(1)由题意,得B(0,m),A(2m,0).
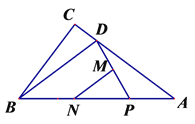
如图,
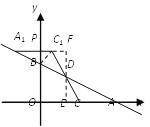
过点D作x轴的垂线,交x轴于点E,交直线A1C1于点F,
易知:DE=![]() m,D(
m,D(![]() m,
m, ![]() m) ,C1(
m) ,C1(![]() m-n,
m-n, ![]() m).
m).
∴![]() m-n=0,
m-n=0,
∴![]() =
=![]() ;
;
(2)由(1)得,当m>3时,点C1在y轴右侧;当2<m<3时,点C1在y轴左侧.
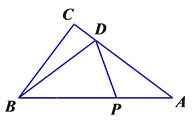
① 当m>3时,设A1C1与y轴交于点P,连接C1B,
由△A1C1D被y轴分得两部分图形的面积比为3:5,
∴S△BA1P:S△BC1P=3:1,
∴A1P:C1P=3,
∴![]() m=3(
m=3(![]() m-4),
m-4),
∴m=![]() .
.
∴y=-![]() x+
x+![]() .
.
② 当2<m<3时,同理可得:y=-![]() x+
x+![]() .
.
综上所述,y=-![]() x+
x+![]() 或y=-
或y=-![]() x+
x+![]() .
.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目