题目内容
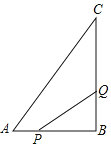
【题目】如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm.点P从点A出发,沿AB边向点B以1cm/s的速度移动;点Q从点B出发,沿BC边向点C以2cm/s的速度移动,设P,Q同时出发,问:
(1)经过几秒后,点P,Q之间距离最小?最小距离是多少?
(2)经过几秒后,△PBQ的面积最大?最大面积是多少?
【答案】(1)经过1.2秒,P、Q的距离最短;为![]() cm;(2)经过3秒,△PBQ的面积最大,最大值是9
cm;(2)经过3秒,△PBQ的面积最大,最大值是9![]() .
.
【解析】
(1)设运动时间为x秒,根据勾股定理求出PQ的代数式,令x=![]() 时求出最小值即可;(2)根据△PBQ=
时求出最小值即可;(2)根据△PBQ=![]() ×PB×BQ=-
×PB×BQ=-![]() +9,当x=3时,
+9,当x=3时,![]() 即可取得最大值.
即可取得最大值.
(1)设运动时间为x秒,
则AP=x,BQ=2x,
∵AB=6,
∴PB=6-x,
则PQ=![]() =
=![]() =
=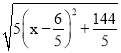 ,
,
∴当x=![]() 时,PQ最短,
时,PQ最短,
∴经过1.2秒,P、Q的距离最短.最短为![]() cm.
cm.
(2)∵△PBQ=![]() ×PB×BQ
×PB×BQ
=![]() (6-x)2x
(6-x)2x
=-![]() +6x
+6x
=-![]() +9
+9
∴当x=3时,![]() 取得最大值9,
取得最大值9,
∴经过3秒,△PBQ的面积最大,最大值是9![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目