题目内容
如图,在Rt△ABC中,∠C=90°,BC=1,AC=2,把边长分别为x1,x2,x3,…,xn的n个正方形依次放入△ABC中,请回答下列问题:(1)按要求填表:
| n | 1 | 2 | 3 |
| xn |
(3)若m,n,p,q是正整数,且xm•xn=xp•xq,试判断m,n,p,q的关系.
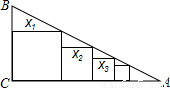
【答案】分析:(1)根据相似三角形的性质就可以求出第一个正方形的边长,其它正方形的边长求法相同;
(2)根据所求xn的一般式进行计算.
解答: 解:(1)设第一个正方形的边长是x,则
解:(1)设第一个正方形的边长是x,则 ,
,
同理得到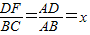 ,
,
两式相加得到
解得x= ,
,
同理解得:第二个的边长是 =
= ,第三个的边长是
,第三个的边长是 =
=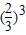 ;
;
(2)依此类推,第n个正方形的边长是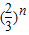 ;
;
(3)∵xm•xn=xp•xq,∴
∴
∴m+n=p+q.
点评:本题主要考查了相似三角形的性质,根据对应边的比相等求出边长,是解决本题的关键.
(2)根据所求xn的一般式进行计算.
解答:
 解:(1)设第一个正方形的边长是x,则
解:(1)设第一个正方形的边长是x,则 ,
,同理得到
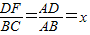 ,
,两式相加得到

解得x=
 ,
,同理解得:第二个的边长是
 =
= ,第三个的边长是
,第三个的边长是 =
=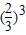 ;
;| n | 1 | 2 | 3 |
| xn |  |  |  |
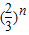 ;
;(3)∵xm•xn=xp•xq,∴

∴

∴m+n=p+q.
点评:本题主要考查了相似三角形的性质,根据对应边的比相等求出边长,是解决本题的关键.

练习册系列答案
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 (2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.
(2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.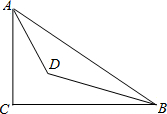 如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离.
如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离.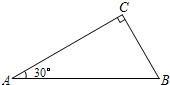 边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.
边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.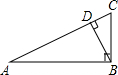 如图,在Rt△ABC中,BD⊥AC,sinA=
如图,在Rt△ABC中,BD⊥AC,sinA=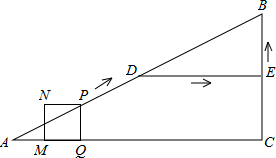 点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).
点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).