题目内容
如果a+b+c=0,且|a|>|b|>|c|.则下列说法中可能成立的是
- A.b为正数,c为负数
- B.c为正数,b为负数
- C.c为正数,a为负数
- D.c为负数,b为正数
C
分析:根据不等式|a|>|b|>|c|及等式a+b+c=0,利用特殊值法,验证即得到正确答案.
解答:由题目答案可知a,b,c三数中只有两正一负或两负一正两种情况,
如果假设两负一正情况合理,
要使a+b+c=0成立,
则必是b<0、c<0、a>0,
否则a+b+c≠0,
但题中并无此答案,则假设不成立,D被否定,
于是应在两正一负的答案中寻找正确答案,
若a,b为正数,c为负数时,
则:|a|+|b|>|c|,
∴a+b+c≠0,
∴A被否定,
若a,c为正数,b为负数时,
则:|a|+|c|>|b|,
∴a+b+c≠0,
∴B被否定,
只有C符合题意,故选C.
点评:本题考查绝对值数及不等式,需要一步步进行推理验证,每一个环节都需要认真推敲.
分析:根据不等式|a|>|b|>|c|及等式a+b+c=0,利用特殊值法,验证即得到正确答案.
解答:由题目答案可知a,b,c三数中只有两正一负或两负一正两种情况,
如果假设两负一正情况合理,
要使a+b+c=0成立,
则必是b<0、c<0、a>0,
否则a+b+c≠0,
但题中并无此答案,则假设不成立,D被否定,
于是应在两正一负的答案中寻找正确答案,
若a,b为正数,c为负数时,
则:|a|+|b|>|c|,
∴a+b+c≠0,
∴A被否定,
若a,c为正数,b为负数时,
则:|a|+|c|>|b|,
∴a+b+c≠0,
∴B被否定,
只有C符合题意,故选C.
点评:本题考查绝对值数及不等式,需要一步步进行推理验证,每一个环节都需要认真推敲.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
如果关于x的不等式组
无解,则m的取值范围是( )
|
| A、m>3 | B、m≥3 |
| C、m<3 | D、m≤3 |
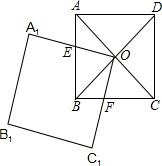 于点E,OC1交BC于点F.
于点E,OC1交BC于点F. ,请问小军至少几次进入迷宫中心?
,请问小军至少几次进入迷宫中心?