题目内容
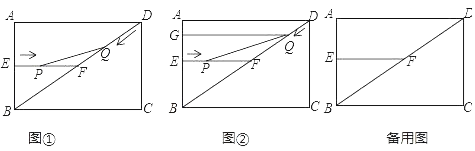
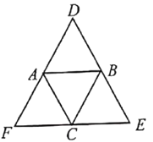
【题目】如图，
是等边三角形，过它的三个顶点分别作对边的平行线，则图中共有______个等边三角形.
【答案】5
【解析】
由△ABC是等边三角形，可得三个内角都是60°，再根据两直线平行内错角相等，可得△AFC、△BCE、△ABD都是等边三角形，而最大的△DEF也是等边三角形，所以共有5个．
解：∵△ABC是等边三角形，
∴∠ABC＝∠BCA＝∠CAB＝60°，
∵DF∥BC，
∴∠FAC＝∠ACB＝60°，∠DAB＝∠ABC＝60°，
同理：∠ACF＝∠BAC＝60°
在△AFC中，∠FAC＝∠ACF＝60°
∴△AFC是等边三角形，
同理可证：△ABD，△BCE都是等边三角形，
因此∠E＝∠F＝∠D＝60°，△DEF是等边三角形，
故有5个等边三角形，
故答案为：5．
练习册系列答案
相关题目
【题目】在全运会射击比赛的选拔赛中，运动员甲10次射击成绩的统计表和扇形统计图如下：
命中环数 | 10 | 9 | 8 | 7 |
命中次数 | 3 | 2 |
（1）根据统计表（图）中提供的信息，补全统计表及扇形统计图；
（2）已知乙运动员10次射击的平均成绩为9环，方差为1．2，如果只能选一人参加比赛，你认为应该派谁去？并说明理由．
