题目内容
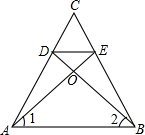 如图,在等腰△ABC中,点D、E分别是两腰AC、BC上的点,连接AE、BD相交于点O,∠1=∠2.
如图,在等腰△ABC中,点D、E分别是两腰AC、BC上的点,连接AE、BD相交于点O,∠1=∠2.(1)求证:OD=OE;
(2)求证:四边形ABED是等腰梯形;
(3)若AB=3DE,△DCE的面积为2,求四边形ABED的面积.
分析:(1)如图,由△ABC是等腰三角形,得到∠BAD=∠ABE,然后利用已知条件证明△ABD≌△BAE,由全等三角形的性质得到BD=AE,又由∠1=∠2得到OA=OB,由此即可证明OD=OE;
(2)由(1)得OD=OE根据等腰三角形的性质得到∠OED=∠ODE,根据三角形的内角和得到∠OED=
(180°-∠DOE),∠1=
(180°-∠AOB),而∠DOE=∠AOB,所以得到∠1=∠OED,然后利用平行线的判定得到DE∥AB,最后证明AD与BE不平行,这样就可以证明梯形ABED是等腰梯形;
(3)由(2)可知DE∥AB,然后得到△DCE∽△ACB,接着利用相似三角形的性质即可求出S△ACB,然后就可以求出S四边形ABED.
(2)由(1)得OD=OE根据等腰三角形的性质得到∠OED=∠ODE,根据三角形的内角和得到∠OED=
| 1 |
| 2 |
| 1 |
| 2 |
(3)由(2)可知DE∥AB,然后得到△DCE∽△ACB,接着利用相似三角形的性质即可求出S△ACB,然后就可以求出S四边形ABED.
解答:(1)证明:如图,∵△ABC是等腰三角形,
∴AC=BC,
∴∠BAD=∠ABE,
又∵AB=BA、∠2=∠1,
∴△ABD≌△BAE(ASA),
∴BD=AE,
又∵∠1=∠2,
∴OA=OB,
∴BD-OB=AE-OA,
即:OD=OE;
(2)证明:由①得OD=OE,
∴∠DOE=∠BOA,
=
,
∴△DOE∽△BOA,
∴∠EDO=∠ABO,
∴DE∥AB,
又∵∠DAB=∠EBA,
∴四边形ABEO为等腰梯形;
(3)解:由(2)可知:DE∥AB,
∴∠CED=∠CBA,∠CDE=∠CAB,
∴△DCE∽△ACB(AA),
∴
=(
)2,
即
=(
)2=
.
∴S△ACB=18,
∴S四边形ABED=S△ACB-S△DCE=18-2=16.
∴AC=BC,
∴∠BAD=∠ABE,
又∵AB=BA、∠2=∠1,
∴△ABD≌△BAE(ASA),
∴BD=AE,
又∵∠1=∠2,
∴OA=OB,
∴BD-OB=AE-OA,
即:OD=OE;
(2)证明:由①得OD=OE,
∴∠DOE=∠BOA,
| DO |
| BO |
| EO |
| AO |
∴△DOE∽△BOA,
∴∠EDO=∠ABO,
∴DE∥AB,
又∵∠DAB=∠EBA,
∴四边形ABEO为等腰梯形;
(3)解:由(2)可知:DE∥AB,
∴∠CED=∠CBA,∠CDE=∠CAB,
∴△DCE∽△ACB(AA),
∴
| S△DCE |
| S△ACB |
| DE |
| AB |
即
| 2 |
| S△ACB |
| DE |
| 3DE |
| 1 |
| 9 |
∴S△ACB=18,
∴S四边形ABED=S△ACB-S△DCE=18-2=16.
点评:此题考查了全等三角形的性质与判定、相似三角形的性质与判定、等腰三角形的性质与判定及等腰梯形的判定,有一定的综合性,要求学生熟练掌握相关的基础知识才能很好解决这类问题.

练习册系列答案
相关题目
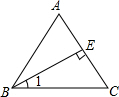 如图,在等腰△ABC中,AB=AC,BE⊥AC,垂足为E,则∠1与∠A的关系式为( )
如图,在等腰△ABC中,AB=AC,BE⊥AC,垂足为E,则∠1与∠A的关系式为( )| A、∠1=∠A | ||
B、∠1=
| ||
| C、∠1=2∠A | ||
| D、无法确定 |
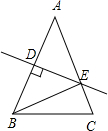 如图,在等腰△ABC中,AB=AC,AB的垂直平分线DE交AB于点D,交另一腰AC于点E,若∠EBC=15°,则∠A=
如图,在等腰△ABC中,AB=AC,AB的垂直平分线DE交AB于点D,交另一腰AC于点E,若∠EBC=15°,则∠A=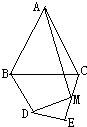 24、如图,在等腰△ABC中,AB=AC,∠ABC=α,在四边形BDEC中,DB=DE,∠BDE=2α,M为CE的中点,连接AM,DM.
24、如图,在等腰△ABC中,AB=AC,∠ABC=α,在四边形BDEC中,DB=DE,∠BDE=2α,M为CE的中点,连接AM,DM.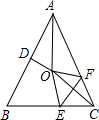 (2012•丽水)如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是
(2012•丽水)如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是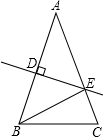 如图,在等腰△ABC中,AB=AC=10cm,直线DE垂直平分AB,分别交AB、AC于D、E两点.若BC=8cm,则△BCE的周长是
如图,在等腰△ABC中,AB=AC=10cm,直线DE垂直平分AB,分别交AB、AC于D、E两点.若BC=8cm,则△BCE的周长是