题目内容
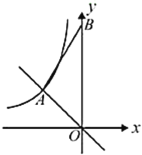
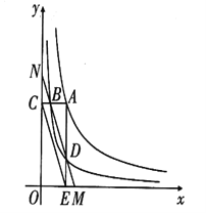
【题目】反比例函数![]() 在第一象限的图象如图所示,过
在第一象限的图象如图所示,过![]() 上任意一点
上任意一点![]() ,作
,作![]() 轴垂线交
轴垂线交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,作
,作![]() 轴垂线,交
轴垂线,交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 分别交
分别交![]() 轴,
轴,![]() 轴于点
轴于点![]() ,则
,则![]() __________.
__________.
【答案】![]()
【解析】
设点A的坐标为(![]() ,
,![]() ),则B(
),则B(![]() ,
,![]() ), C(
), C(![]() ,
,![]() ), D(
), D(![]() ,
,![]() ), E(
), E(![]() ,
,![]() ),利用待定系数法求得直线BD的解析式为
),利用待定系数法求得直线BD的解析式为![]() ,求得点M、N的坐标分别为(
,求得点M、N的坐标分别为(![]() ,
,![]() ),(
),(![]() ,
,![]() ),由此即可得出
),由此即可得出![]() ,结合∠COE=∠NOM即可证出△COE∽△NOM,再根据相似三角形的性质即可得出结论.
,结合∠COE=∠NOM即可证出△COE∽△NOM,再根据相似三角形的性质即可得出结论.
设点A的坐标为(![]() ,
,![]() ),
),
∵AC⊥![]() 轴交双曲线
轴交双曲线![]() 于点B,
于点B,
∴点A、B、C的纵坐标都是![]() ,
,
∴点B的坐标为(![]() ,
,![]() ), 点C的坐标为(
), 点C的坐标为(![]() ,
,![]() ),
),
∵AE⊥![]() 轴交双曲线
轴交双曲线![]() 于点D,
于点D,
∴点A、D、E的横坐标都是![]() ,
,
∴点D的坐标为(![]() ,
,![]() ), 点E的坐标为(
), 点E的坐标为(![]() ,
,![]() ),
),
设直线BD的解析式为![]() ,把B(
,把B(![]() ,
,![]() ), D(
), D(![]() ,
,![]() )代入得:
)代入得:
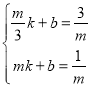 ,
,
解得: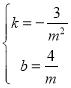 ,
,
∴直线BD的解析式为![]() ,
,
令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,
,
∴点M的坐标为(![]() ,
,![]() ),点N的坐标为(
),点N的坐标为(![]() ,
,![]() ),
),
∴OC=![]() ,ON=
,ON=![]() ,OE=
,OE=![]() ,OM=
,OM=![]() ,
,
∴![]() ,
,
又∵∠COE=∠NOM=90![]() ,
,
∴△COE∽△NOM,
∴![]() ,
,
故答案为:![]() .
.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如表:
的部分对应值如表:
|
|
|
|
|
|
|
|
|
|
|
|
下列结论:![]() 抛物线的开口向上;②抛物线的对称轴为直线
抛物线的开口向上;②抛物线的对称轴为直线![]() ;③当
;③当![]() 时,
时,![]() ;④抛物线与
;④抛物线与![]() 轴的两个交点间的距离是
轴的两个交点间的距离是![]() ;⑤若
;⑤若![]() 是抛物线上两点,则
是抛物线上两点,则![]() ,其中正确的个数是( )
,其中正确的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()