Question

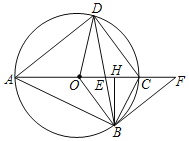
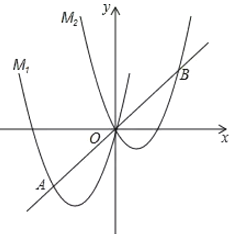
【题目】如图，△ABC中，AB=AC，以AB为直径的⊙O分别交AC、BC于点D、F，连接BD交OF于点E．

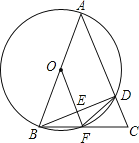
（1）求证：OF⊥BD；

（2）若AB=，DF=，求AD的长．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）连接AF．根据直径所对的圆周角是直角、等腰三角形的性质以及平行线的性质即可证明；
（2）设AD=x．根据圆周角定理的推论和勾股定理进行求解．

解：（1）证明：连接AF，如图所示：

∵AB是⊙O的直径，

∴∠AFB=∠ADB=90°，

∵AB=AC，

∴FC=FB．

∵OA=OB，

∴OD∥AC．

∴∠OEB=∠ADB=90°，

∴OF⊥BD．

（2）设AD=x，

∵OF⊥BD，

∴可得OF是BD的中垂线，

∴FD=FB，

∴∠1=∠2，

∴BF=DF=，

∵OF⊥DB，

∴ED=EB．

∴OE=AD=，FE=OF﹣OE=，

在Rt△FEB中，BE2=EB2﹣FE2=；

在Rt△OFB中，BE2=OB2﹣OE2=；

∴=

解得：x=，

即AD=．