题目内容
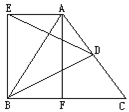
【题目】已知,如图,等边△ABC中,AD=DC,BF=FC,△BDE是等边三角形.求证:四边形AEBF是矩形.
【答案】见解析
【解析】
根据等边三角形的性质可得AF=BD=BE,再求出∠EBF=∠AFB=90°,连接EF,然后利用“边角边”证明△ABF和△EFB全等,根据全等三角形对应边相等可得AB=EF,再证出四边形AEBF是平行四边形,然后根据对角线相等的平行四边形是矩形证明即可.
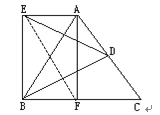
证明:连接EF,
∵等边△ABC中,点D是AC的中点,F是BC的中点,
∴AF=BD,∠CBD=30°,∠AFB=90°
∵△BDE是等边三角形,
∴BE=BD,∠DBE=60°,
∴∠EBF=∠DBE+∠CBD=90°
∴AF=BD=BE,∠EBF=∠AFB,
在△ABF和△EFB中,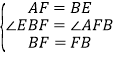
∴△ABF≌△EFB(SAS),
∴AB=EF,
∵∠AFB=∠EBF=90°,
∴AF∥BE,
又∵AF=BE,
∴四边形AEBF是平行四边形,
∵AB=EF,
∴四边形AEBF是矩形,
故AB=EF,且四边形AEBF是矩形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】探究题.
用棋子摆成的“T”字形图如图所示:

(1)填写下表:
图形序号 | ① | ② | ③ | ④ | … | ⑩ |
每个图案中棋子个数 | 5 | 8 | … |
(2)写出第n个“T”字形图案中棋子的个数_________________(用含n的代数式表示);
(3)第20个“T”字形图案共有棋子____________个?
(4)计算前20个“T”字形图案中棋子的总个数.
(提示:请你先思考下列问题:第1个图案与第20个图案中共有多少个棋子?第2个图案与第19个图案中共有多少个棋子?第3个图案与第18个图案呢?)