题目内容
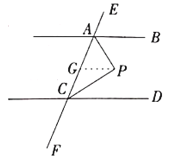
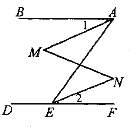
【题目】如图,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N.下面是推理过程,请你填空:
解:∵∠BAE+∠AED=180° (已知) ,
∴AB//DE( ),
∴∠BAE= ( )
又 ∵∠1=∠2(已知)
∴∠BAE-∠1= - (等式性质),
即∠MAE=∠NEA,
∴ ∥ ( ),
∴∠M=∠N(两直线平行,内错角相等).
【答案】同旁内角互补,两直线平行,∠AEF, 两直线平行,内错角相等,∠AEF, ∠2,AM,EN,内错角相等, 两直线平行
【解析】
由已知易得AB∥CD,则∠BAE=∠AEF,又∠1=∠2,所以∠MAE=∠AEN,则AM∥EN,故∠M=∠N.
∵∠BAE+∠AED=180°(已知)
∴AB∥CD(同旁内角互补,两直线平行)
∠BAE=∠AEF(两直线平行,内错角相等)
又∵∠1=∠2,
∴∠BAE∠1=∠AEF∠2,
即∠MAE=∠NEA,
∴AM∥EN,(内错角相等,两直线平行)
∴∠M=∠N(两直线平行,内错角相等)

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目