��Ŀ����
����Ŀ������������12�֣���ͼ���������ϵ�A��B��C��ʾ�����ֱ�Ϊ-2��1��6����A���B֮��ľ����ʾΪAB����B���C֮��ľ����ʾΪBC����A���C֮��ľ����ʾΪAC��
��1����AB=______��BC=______��AC=______��
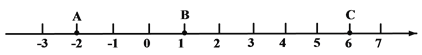
��2����A��B��C��ʼ���������˶�������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�5����λ���ȵ��ٶ������˶���������BC��AB��ֵ�Ƿ������˶�ʱ��t�ı仯���ı䣿���仯����˵����������������������ֵ��
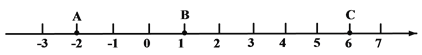
��3���ɵڣ�1��С����Է�����AB+BC=AC������C��ÿ��3����λ���ȵ��ٶ������˶���ͬʱ����A�͵�B�ֱ���ÿ��1����λ���Ⱥ�ÿ��2����λ���ȵ��ٶ������˶��������������˶�ʱ��t�ı仯��AB��BC��AC֮���Ƿ���������ڣ�1����������ϵ����˵��������
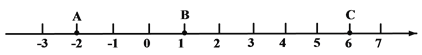
���𰸡���1��AB=3��BC=5��AC=8����2��BC��AB��ֵ��������ʱ��t�ı仯���ı���BC��AB=2 ��
��3����t��1ʱ��AB+BC=AC����1��t��2ʱ��BC+AC=AB����t��2ʱ��AB+AC=BC��
�������������������1�����ݵ�A��B��C�������ϵ�λ�ã�д��AB��BC��AC�ij��ȣ�
��2�����BC��AB��ֵ��Ȼ�����BC-AB��ֵ���жϼ��ɣ�
��3���ֱ��ʾ��AB��BC��AC�ij��ȣ�Ȼ���������۵ó�֮��Ĺ�ϵ��
�����������1����ͼ�ɵã�AB=3��BC=5��AC=8��
��2��BC-AB=��5t-2t+5��-��t+2t+3��=2��
��BC-AB��ֵ��������ʱ��t�ı仯���ı䣻
��3��������ã�AB=t+3��
BC=5-5t��t��1ʱ����BC=5t-5��t��1ʱ����
AC=8-4t��t��2ʱ����AC=4t-8��t��2ʱ����
��t��1ʱ��AB+BC=��t+3��+��5-5t��=8-4t=AC��
��1��t��2ʱ��BC+AC=��5t-5��+��8-4t��=t+3=AB��
��t��2ʱ��AB+AC=��t+3��+��4t-8��=5t-5=BC��

 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�����Ŀ����������Ⱥ���н���5�·���������������������¼��(��λ����Ԫ)
���� | 14�� | 15�� | 16�� | 17�� | 18�� | 19�� | 20�� |
�������� | 0.20 | 0.17 | 0.23 | 0.21 | 0.23 | 0.18 | 0.25 |
�ɹ�����Ⱥ������һ���µ�������(����)
A. 6.51��Ԫ B. 6.42��Ԫ C. 1.47��Ԫ D. 5.88��Ԫ