题目内容
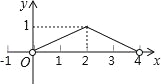
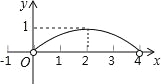
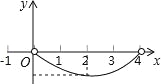
【题目】(本题满分11分)让我们一起探索有趣的“皮克定理”:用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形.设格点多边形的面积为S,它各边上格点的个数和为x.
 .
.
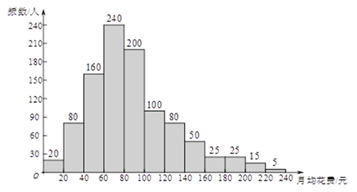
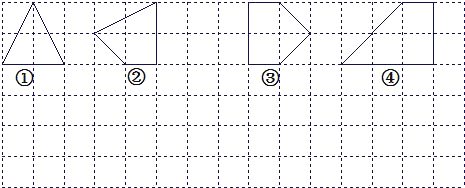
(1)上图中的格点多边形,其内部都只有一个格点,请完成下表,并写出S与x之间的关系式:S=______.

(2)探索:在上面网格图中画出四个格点多边形,其内部都只有两个格点,并写出所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式:S=______;
(3)猜想:当格点多边形内部有且只有n个格点时,S与x之间的关系式是:S=______.
【答案】(1)![]() ,3 ,
,3 , ![]() ;(2)作图见解析,
;(2)作图见解析, ![]() +1;(3)
+1;(3)![]() +(n-1).
+(n-1).
【解析】试题分析:(1)分别算出②和③的面积,再探索规律;(2)先画出四个图形,再求出四个图形的面积,最后探索面积S和x的关系;(3)由(1)(2)问求出的S与x的关系探索规律.
解:(1)图②的面积为S=4-![]() ×1×2-
×1×2-![]() ×1×1=
×1×1=![]() ,图③的面积为S=4-
,图③的面积为S=4-![]() ×1×1-
×1×1-![]() ×1×1=3,
×1×1=3,
根据2, ![]() ,3,4对应4,5,6,8,可知S和x的关系为S=
,3,4对应4,5,6,8,可知S和x的关系为S=![]() x;
x;
故答案为![]() ,3,
,3, ![]() .
.
(2)如图,分别画出四个格点多边形⑤⑥⑦⑧,其内部都只有两个格点.
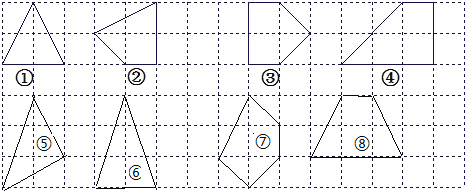
图⑤中x=3,S=![]() ;图⑥中,x=4,S=3;图⑦中,x=5,S=
;图⑥中,x=4,S=3;图⑦中,x=5,S=![]() ;图⑧中,x=6,S=4.
;图⑧中,x=6,S=4.
则可知此时S= ![]() +1;
+1;
(3)当n=1时,S= ![]() ;
;
当n=2时,S= ![]() +1.
+1.
则可知![]() +(n-1).
+(n-1).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目