Question

【题目】如图：公路旁有两个高度相等的路灯AB、CD．小明同学上午上学时发现路灯B在太阳光下的影子恰好落到里程碑E处，他自己的影子恰好落在路灯CD的底部C处．晚自习放学时，站在上午同一个地方，发现在路灯CD的灯光下自己的影子恰好落在里程碑E处．

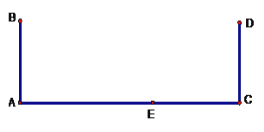
（1）在图中画出小明的位置，并画出光线，标明（太阳光、灯光）．

（2）若AC距离为80米，小明身高为1.5米，小明离里程碑E恰好5米，求路灯高．

Answer 1

【答案】（1）画图见解析，详情见解析；（2）6米；

【解析】

(1)由图，GH所在位置就是小明的位置，所以DG为灯光，连接太阳光线BE，过点C作BE的平行线CG，即图中BE、CG是太阳光，DG为灯光；

（2）由GH⊥AC，CD⊥AC，可得GH∥CD，从而得△EGH∽△EDC，即；又CG∥BE，可得∠GCE=∠BEA，因为GH⊥AC，AB⊥AC，所以∠BAC=∠GHC=90°，推出∠GCE=∠BEA，∠BAC=∠GHC，得到△GCH∽△BEA，即；再根据题意可得GH=1.5米，EH=5米，AC=80米，AB=CD，可设AB=x米，因为，，AB=CD，可得，即，把数值代入和得，

解得x=6，即AB=CD=6米；

解：

（1）如图，GH所在位置就是小明的位置，连结BE、DE，过C作CG∥BE与DE相交于点G，过G作GH⊥AC，即图中BE、CG是太阳光，DG为灯光；

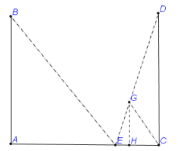
（2）如图，GH所在位置就是小明的位置，

连结BE、DE，过C作CG∥BE与DE相交于点G，过G作GH⊥AC，即图中BE、CG是太阳光，DG为灯光；

∵GH⊥AC，CD⊥AC，

∴GH∥CD，

∴△EGH∽△EDC，

∴，

∵CG∥BE，

∴∠GCE=∠BEA，

∵GH⊥AC，AB⊥AC，

∴∠BAC=∠GHC=90°，

∵∠GCE=∠BEA，∠BAC=∠GHC，

∴△GCH∽△BEA，

∴，

根据题意可得GH=1.5米，EH=5米，AC=80米，AB=CD，可设AB=x米，

∵，，AB=CD，

∴，

∴，

将GH=1.5米，EH=5米，AC=80米，AB=CD，AB=x米代入和得，

，，

联立两式，解得x=6，

即AB=CD=6米，

路灯的高为6米；