题目内容
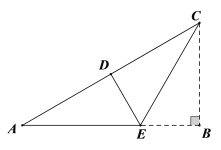
【题目】如图所示△ABC,AB=AC,AD⊥BC,点E、F分别是AB、AC的中点.

(1)求证:四边形AEDF是菱形;
(2)若四边形AEDF的周长为12,两条对角线的和等于7,四边形AEDF的面积记为S1,三 角形ABC的面积记为S2,S1与S2有何数量关系_____.(直接填答案)
【答案】(1)详见解析;(2)2S1=S2.
【解析】
(1)根据直角三角形斜边上中线的性质,得出DE=![]() AB=AE,DF=
AB=AE,DF=![]() AC=AF,再根据AB=AC,点E、F分别是AB、AC的中点,即可得到AE=AF=DE=DF,进而判定四边形AEDF是菱形;(2)利用三角形的中线把三角形分成面积相等的两部分即可解答.
AC=AF,再根据AB=AC,点E、F分别是AB、AC的中点,即可得到AE=AF=DE=DF,进而判定四边形AEDF是菱形;(2)利用三角形的中线把三角形分成面积相等的两部分即可解答.
(1)证明:∵AD⊥BC,点E、F分别是AB、AC的中点,
∴Rt△ABD中,DE=![]() AB=AE,
AB=AE,
Rt△ACD中,DF=![]() AC=AF,
AC=AF,
又∵AB=AC,点E、F分别是AB、AC的中点,
∴AE=AF,
∴AE=AF=DE=DF,
∴四边形AEDF是菱形;
(2)2S1=S2
∵点E、F分别是AB、AC的中点,
∴![]() ,
,
∴![]() ,
,
即2S1=S2.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目