题目内容
【题目】某大学生利用暑假40天社会实践进行创业，他在网上开了一家微店，销售推广一种成本为25元/件的新型商品.在40天内，其销售单价n（元/件）与时间x（天）的关系式是：当1≤x≤20时，
；当21≤x≤40时，
.这40天中的日销售量m（件）与时间x（天）符合函数关系，具体情况记录如下表（天数为整数）:
时间x（天） | 5 | 10 | 15 | 20 | 25 | … |
日销售量m(件） | 45 | 40 | 35 | 30 | 25 | … |
（1）请求出日销售量m（件）与时间x（天）之间的函数关系式；
（2）若设该同学微店日销售利润为w元，试写出日销售利润w（元）与时间x（天）的函数关系式；
（3）求这40天中该同学微店日销售利润不低于640元有多少天？
【答案】（1）m=-x+50；（2）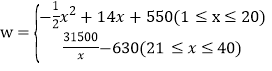
；（3）这40天中该同学微店日销售利润不低于640元有13天.
【解析】(1)、首先设日销售量m（件）与时间x（天）之间的函数关系式为m=kx+b，然后利用待定系数法求出函数解析式；(2)、根据1≤x≤20和21≤x≤40两种情况分别求出w与x的函数关系式；(3)、分两段函数分别求出x的值，然后得出不等式，从而求出天数．
(1)、设日销售量m（件）与时间x（天）之间的函数关系式为m=kx+b，
把x=5,m=45代入得5k+b=45①， 把x=10,m=40代入得10k+b=40②，
将①②联立方程组解得
， ∴m=-x+50，
当x=15时m=35,当x=20时m=30,当x=25时m=25，
因此，经验证日销售量m（件）与时间x（天）之间的函数关系式为m=-x+50；
(2)、当1≤x≤20时，w=
=
=
，
当21≤x≤40时，w=
=
=
，
∴w关于x的函数关系式为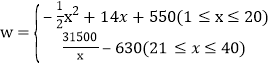
；
(3)、当w=640时，
∴
，解得x1=10,x2=18，
∴当1≤x≤20时,日利润不低于640元有：18-10+1=9（天）.
若
时，则x≈24.8
∴当21≤x≤40时,日利润不低于640元有：24-21+1=4（天）， ∴9+4=13（天）
∴这40天中该同学微店日销售利润不低于640元有13天.
