Question

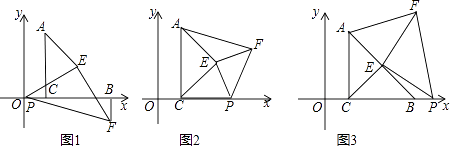
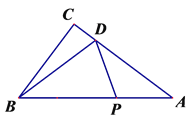
【题目】已知二次函数y＝ax2－8ax(a＜0)的图像与x轴的正半轴交于点A，它的顶点为P．点C为y轴正半轴上一点，直线AC与该图像的另一交点为B，与过点P且垂直于x轴的直线交于点D，且CB：AB＝1：7．

（1）求点A的坐标及点C的坐标(用含a的代数式表示)；

（2）连接BP，若△BDP与△AOC相似（点O为原点），求此二次函数的关系式．

Answer 1

【答案】（1）A(8，0), C(0，－8a)．(2)

【解析】试题分析：（1）由y＝ax2－8ax可得A(8，0)，由CB：AB＝1：7得点B的横坐标为1，故B(1，－7a)，C(0，－8a)．

（2）对称轴与x轴交于点H，过点B作BF⊥PD于点F，易知，BF＝3，AH＝4，DH＝－4a，则FD＝－3a， PF＝－9a，由相似，可知：BF2=DF·PF，从而求得a的值，故可求函数关系式.

试题解析：（1）P(4，－16a)，A(8，0)，

∵CB：AB＝1：7，

∴点B的横坐标为1

∴B(1，－7a)，

∴C(0，－8a)．

（2）∵△AOC为直角三角形，

∴只可能∠PBD＝90°，且△AOC∽△PBD．………（5分）

设对称轴与x轴交于点H，过点B作BF⊥PD于点F，

易知，BF＝3，AH＝4，DH＝－4a，则FD＝－3a，

∴PF＝－9a，

由相似，可知：BF2＝DF·PF，

∴9＝－9a·(－3a)，

∴a＝， a＝－ (舍去)．

∴y＝－x2－x．