题目内容
【题目】如图,过△ABC的顶点A分别作∠ACB及其外角的平分线的垂线,垂直分布为E、F,连接EF交AB于点M,交AC于点N,求证:
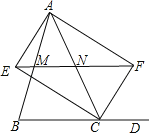
(1)四边形AECF是矩形;
(2)MN=![]() BC.
BC.
【答案】见解析
【解析】
试题分析:(1)由角平分线的定义和邻补角定义得出∠ECF=90°,由AE⊥CE,AF⊥CF,得出∠AEC=∠AFC=90°,即可得出四边形AECF是矩形;
(2)由矩形的性质得出EN=FN,AN=CN=![]() AC,由直角三角形斜边上的中线性质得出CN=
AC,由直角三角形斜边上的中线性质得出CN=![]() EF=EN,由等腰三角形的性质得出∠NEC=∠ACE=∠BCE,证出EN∥BC,得出△AMN∽△ABC,由相似三角形的对应边成比例即可得出结论.
EF=EN,由等腰三角形的性质得出∠NEC=∠ACE=∠BCE,证出EN∥BC,得出△AMN∽△ABC,由相似三角形的对应边成比例即可得出结论.
证明:(1)∵CE平分∠ACB,CF平分∠ACD,
∴∠ACE=∠BCE=![]() ∠ACB,∠ACF=
∠ACB,∠ACF=![]() ∠ACD,
∠ACD,
∵∠ACB+∠ACD=180°,
∴∠ACE+∠ACF=90°,
即∠ECF=90°,
又∵AE⊥CE,AF⊥CF,
∴∠AEC=∠AFC=90°,
∴四边形AECF是矩形;
(2)∵四边形AECF是矩形,
∴EN=FN,AN=CN=![]() AC,
AC,
∴CN=![]() EF=EN,
EF=EN,
∴∠NEC=∠ACE=∠BCE,
∴EN∥BC,
∴△AMN∽△ABC,
∴![]() =
=![]() =
=![]() ,
,
∴MN=![]() BC.
BC.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目