题目内容
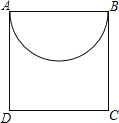
【题目】如图，四边形ABCD为正方形，边长为4，点F在AB边上，E为射线AD上一点，正方形ABCD沿直线EF折叠，点A落在G处，已知点G恰好在以AB为直径的圆上，则CG的最小值等于（ ）
A．0 B．2
C．4﹣2 D．2﹣2
【答案】D
【解析】
试题分析：先根据题意画出图形，由翻折的性质可知AF=FG，AG⊥OE，∠OGE=90°，由垂径定理可知点O为半圆的圆心，从而得到OB=OG=2，依据勾股定理可求得OC的长，最后依据GC=OC﹣OG求解即可．
解：如图所示：
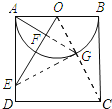
由翻折的性质可知：AF=FG，AG⊥OE，∠OAE=∠OGE=90°．
∵AF=FG，AG⊥OE，
∴点O是圆半圆的圆心．
∴OG=OA=OB=2．
在△OBC中，由勾股定理可知：OC=
=
=2
．
∵当点O、G、C在一条直线上时，GC有最小值，
∴CG的最小值=OC﹣OG=2﹣2．
故选：D．
练习册系列答案
阅读快车系列答案
相关题目
