题目内容
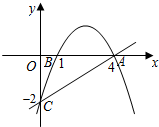 如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.
如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.(1)求出抛物线的解析式;
(2)P是抛物线上一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;
(3)在直线AC上方的抛物线上有一点D,使得△DCA的面积最大,求出点D的坐标.
分析:(1)本题需先根据已知条件,过C点,设出该抛物线的解析式为y=ax2+bx-2,再根据过A,B两点,即可得出结果.
(2)本题首先判断出存在,首先设出横坐标和纵坐标,从而得出PA的解析式,再分三种情况进行讨论,当
=
=
时和
=
=
时,当P,C重合时,△APM≌△ACO,分别求出点P的坐标即可.
(3)本题需先根据题意设出D点的横坐标和D点的纵坐标,再过D作y轴的平行线交AC于E,再由题意可求得直线AC的解析式为,即可求出E点的坐标,从而得出结果即可.
(2)本题首先判断出存在,首先设出横坐标和纵坐标,从而得出PA的解析式,再分三种情况进行讨论,当
| AM |
| PM |
| AO |
| OC |
| 2 |
| 1 |
| AM |
| PM |
| OC |
| OA |
| 1 |
| 2 |
(3)本题需先根据题意设出D点的横坐标和D点的纵坐标,再过D作y轴的平行线交AC于E,再由题意可求得直线AC的解析式为,即可求出E点的坐标,从而得出结果即可.
解答:解:(1)∵该抛物线过点C(0,-2),
∴可设该抛物线的解析式为y=ax2+bx-2.
将A(4,0),B(1,0)代入,
得
,
解得
,
∴此抛物线的解析式为y=-
x2+
x-2;
(2)存在.如图,设P点的横坐标为m,
则P点的纵坐标为-
m2+
m-2,
当1<m<4时,AM=4-m,PM=-
m2+
m-2.
又∵∠COA=∠PMA=90°,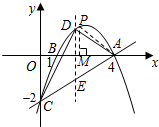
∴①当
=
,
∵C在抛物线上,
∴OC=2,
∵OA=4,
∴
=
=
,
∴△APM∽△ACO,
即4-m=2(-
m2+
m-2).
解得m1=2,m2=4(舍去),
∴P(2,1).
②当
=
=
时,△APM∽△CAO,即2(4-m)=-
m2+
m-2.
解得m1=4,m2=5(均不合题意,舍去)
∴当1<m<4时,P(2,1),
当m>4时,AM=m-4,PM=
m2-
m+2,
①
=
=
或②
=
=2,
把P(m,-
m2+
m-2)代入得:2(
m2-
m+2)=m-4,2(m-4)=
m2-
m+2,
解得:第一个方程的解是m=-2-2
<4(舍去)m=-2+2
<4(舍去),
第二个方程的解是m=5,m=4(舍去)
求出m=5,-
m2+
m-2=-2,
则P(5,-2),
当m<1时,AM=4-m,PM=
m2-
m+2.
①
=
=
或
=
=2,
则:2(
m2-
m+2)=4-m,2(4-m)=
m2-
m+2,
解得:第一个方程的解是m=0(舍去),m=4(舍去),第二个方程的解是m=4(舍去),m=-3,
m=-3时,-
m2+
m-2=-14,
则P(-3,-14),
综上所述,符合条件的点P为(2,1)或(5,-2)或(-3,-14),
(3)如图,设D点的横坐标为t(0<t<4),则D点的纵坐标为|-
t2+
t-2|.
过D作y轴的平行线交AC于E.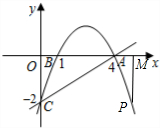
由题意可求得直线AC的解析式为y=
x-2.
∴E点的坐标为(t,
t-2).
∴DE=-
t2+
t-2-(
t-2)=-
t2+2t,
∴S△DAC=S△DCE+S△DEA=
DE•h+
DE•(4-h)=
DE•4,
∴S△DAC=
×(-
t2+2t)×4=-t2+4t=-(t-2)2+4,
∴当t=2时,△DAC面积最大,
∴D(2,1).
∴可设该抛物线的解析式为y=ax2+bx-2.
将A(4,0),B(1,0)代入,
得
|
解得
|
∴此抛物线的解析式为y=-
| 1 |
| 2 |
| 5 |
| 2 |
(2)存在.如图,设P点的横坐标为m,
则P点的纵坐标为-
| 1 |
| 2 |
| 5 |
| 2 |
当1<m<4时,AM=4-m,PM=-
| 1 |
| 2 |
| 5 |
| 2 |
又∵∠COA=∠PMA=90°,

∴①当
| AM |
| PM |
| AO |
| OC |
∵C在抛物线上,
∴OC=2,
∵OA=4,
∴
| AM |
| PM |
| AO |
| OC |
| 2 |
| 1 |
∴△APM∽△ACO,
即4-m=2(-
| 1 |
| 2 |
| 5 |
| 2 |
解得m1=2,m2=4(舍去),
∴P(2,1).
②当
| AM |
| PM |
| OC |
| OA |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
解得m1=4,m2=5(均不合题意,舍去)
∴当1<m<4时,P(2,1),
当m>4时,AM=m-4,PM=
| 1 |
| 2 |
| 5 |
| 2 |
①
| PM |
| AM |
| OC |
| OA |
| 1 |
| 2 |
| PM |
| AM |
| OA |
| OC |
把P(m,-
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
解得:第一个方程的解是m=-2-2
| 3 |
| 3 |
第二个方程的解是m=5,m=4(舍去)
求出m=5,-
| 1 |
| 2 |
| 5 |
| 2 |
则P(5,-2),
当m<1时,AM=4-m,PM=
| 1 |
| 2 |
| 5 |
| 2 |
①
| PM |
| AM |
| OC |
| OA |
| 1 |
| 2 |
| PM |
| AM |
| OA |
| OC |
则:2(
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
解得:第一个方程的解是m=0(舍去),m=4(舍去),第二个方程的解是m=4(舍去),m=-3,
m=-3时,-
| 1 |
| 2 |
| 5 |
| 2 |
则P(-3,-14),
综上所述,符合条件的点P为(2,1)或(5,-2)或(-3,-14),
(3)如图,设D点的横坐标为t(0<t<4),则D点的纵坐标为|-
| 1 |
| 2 |
| 5 |
| 2 |
过D作y轴的平行线交AC于E.

由题意可求得直线AC的解析式为y=
| 1 |
| 2 |
∴E点的坐标为(t,
| 1 |
| 2 |
∴DE=-
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△DAC=S△DCE+S△DEA=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△DAC=
| 1 |
| 2 |
| 1 |
| 2 |
∴当t=2时,△DAC面积最大,
∴D(2,1).
点评:本题主要考查了二次函数解析式的确定、函数图象交点的求法等知识点,主要考查学生数形结合的数学思想方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
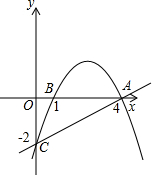 如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.
如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点. 如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点,
如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点, (2013•苏州一模)如图,抛物线经过A,C,D三点,且三点坐标为A(-1,0),C(0,5),D(2,5),抛物线与x轴的另一个交点为B点,点F为y轴上一动点,作平行四边形DFBG,
(2013•苏州一模)如图,抛物线经过A,C,D三点,且三点坐标为A(-1,0),C(0,5),D(2,5),抛物线与x轴的另一个交点为B点,点F为y轴上一动点,作平行四边形DFBG, (2013•高要市二模)已知:如图,抛物线经过点O、A、B三点,四边形OABC是直角梯形,其中点A在x轴上,点C在y轴上,BC∥OA,A(12,0)、B(4,8).
(2013•高要市二模)已知:如图,抛物线经过点O、A、B三点,四边形OABC是直角梯形,其中点A在x轴上,点C在y轴上,BC∥OA,A(12,0)、B(4,8).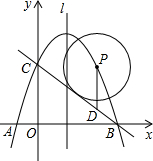 如图,抛物线经过A(-2,0)、B(8,0)两点,与y轴正半轴交与点C,且AB=BC,点P为第一象限内抛物线上一动点(不与B、C重合),设点P的坐标为(m,n).
如图,抛物线经过A(-2,0)、B(8,0)两点,与y轴正半轴交与点C,且AB=BC,点P为第一象限内抛物线上一动点(不与B、C重合),设点P的坐标为(m,n).