题目内容
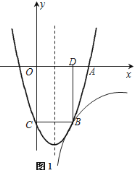
【题目】如图![]() ,二次函数
,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,并过点
,并过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .抛物线
.抛物线![]() 和反比例函数
和反比例函数![]() 的图象都经过点
的图象都经过点![]() ,四边形
,四边形![]() 的面积是
的面积是![]() .
.
![]() 求反比例函数、二次函数的解析式及抛物线的对称轴;
求反比例函数、二次函数的解析式及抛物线的对称轴;
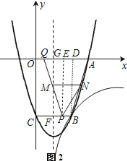
![]() 如图
如图![]() ,点
,点![]() 从
从![]() 点出发以每秒
点出发以每秒![]() 个单位的速度沿线段
个单位的速度沿线段![]() 向
向![]() 点运动,点
点运动,点![]() 从
从![]() 点出发以相同的速度沿线段img src="http://thumb.zyjl.cn/questionBank/Upload/2019/05/12/08/1a8f9afd/SYS201905120854095644903087_ST/SYS201905120854095644903087_ST.023.png" width="24" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />向
点出发以相同的速度沿线段img src="http://thumb.zyjl.cn/questionBank/Upload/2019/05/12/08/1a8f9afd/SYS201905120854095644903087_ST/SYS201905120854095644903087_ST.023.png" width="24" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />向![]() 点运动,其中一个动点到达端点时,另一个也随之停止运动.设运动时间为
点运动,其中一个动点到达端点时,另一个也随之停止运动.设运动时间为![]() 秒.
秒.
①当![]() 为何值时,四边形
为何值时,四边形![]() 为等腰梯形;
为等腰梯形;
②设![]() 与对称轴的交点为
与对称轴的交点为![]() ,过
,过![]() 点作
点作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,设四边形
,设四边形![]() 的面积为
的面积为![]() ,求面积
,求面积![]() 关于时间
关于时间![]() 的函数解析式,并指出
的函数解析式,并指出![]() 的取值范围;当
的取值范围;当![]() 为何值时,
为何值时,![]() 有最大值或最小值.
有最大值或最小值.

【答案】![]()
![]() ,
,![]() ①当
①当![]() 秒时,四边形
秒时,四边形![]() 为等腰梯形②当
为等腰梯形②当![]() 秒时,面积
秒时,面积![]() 有最小值
有最小值![]() .
.
【解析】
(1)根据反比例函数的比例系数k的几何意义可求出k,从而可求出点B的坐标,然后运用待定系数法就可求出二次函数的解析式,由此可求出对称轴方程;
(2)①过点P作PE⊥OA,垂足为E,如图2,易证BC∥OA,要使四边形ABPQ为等腰梯形,只需PQ=AB,只需QE=AD=1,由此即可求出t的值;②如图2,易证△MFP≌△MGQ,则有MF=MG,从而可求出S△BPN(用t表示),然后只需求出S四边形ABPQ,并运用割补法就可得到S关于t的函数解析式,然后只需利用该函数的增减性就可解决问题.
![]() 如图
如图![]() ,
,
∵四边形![]() 的面积是
的面积是![]()
,
∴![]() ,
,
∴反比例函数的解析式为![]() .
.
∵反比例函数![]() 的图象经过点
的图象经过点![]() ,
,
∴![]() ,
,
解得![]() .
.
∴![]() .
.
将点![]() ,
,![]() 代入
代入![]() ,得
,得
![]()
解得:![]() ,
,
∴二次函数的解析式![]() .
.
则抛物线的对称轴为![]() ;
;![]() ①由题意可知:
①由题意可知:![]() .
.
∵点![]() ,点
,点![]() 的纵坐标相等,
的纵坐标相等,
∴![]() .
.
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,如图
,如图![]() .
.
要使四边形![]() 为等腰梯形,只需
为等腰梯形,只需![]() .
.
即![]() .
.
又![]() ,
,
∴![]() .
.
解得![]() ,
,
∴当![]() 秒时,四边形
秒时,四边形![]() 为等腰梯形.
为等腰梯形.
②设对称轴与![]() 、
、![]() 轴的交点分别为
轴的交点分别为![]() 、
、![]() ,如图
,如图![]() .
.
∵对称轴![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
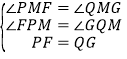
∴![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]() .
.
∵![]()
![]()
![]() ,
,
∴![]()
![]() .
.
∵![]() ,
,![]() ,
,
∴点![]() 运动到点
运动到点![]() 时停止运动,需要
时停止运动,需要![]() 秒,
秒,
∴![]() .
.
∵![]() ,
,
∴当![]() 秒时,面积
秒时,面积![]() 有最小值
有最小值![]() .
.








