题目内容
【题目】定义:有一个角是其邻角一半的圆内接四边形叫做圆内倍角四边形.
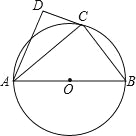
(1)如图1,四边形ABCD内接于⊙O,∠DCB﹣∠ADC=∠A,求证:四边形ABCD为圆内接倍角四边形;
(2)在(1)的条件下,⊙O半径为5.
①若AD为直径,且sinA=![]() ,求BC的长;
,求BC的长;
②若四边形ABCD中有一个角为60°,且BC=CD,则四边形ABCD的面积是 ;
(3)在(1)的条件下,记AB=a,BC=b,CD=c,AD=d,求证:d2﹣b2=ab+cd.

【答案】(1)见解析;(2)①BC=6,②![]() 或
或![]() ;(3)见解析
;(3)见解析
【解析】
(1)先判断出∠ADC=180°﹣2∠A.进而判断出∠ABC=2∠A,即可得出结论;
(2)①先用锐角三角函数求出BD,进而得出AB,由(1)得出∠ADB=∠BDC,即可得出结论;
②分两种情况:利用面积和差即可得出结论;
(3)先得出BE=BC=b,DE=DA=b,进而得出CE=d﹣c,再判断出△EBC∽△EDA,即可得出结论.
(1)设∠A=α,则∠DCB=180°﹣α.
∵∠DCB﹣∠ADC=∠A,∴∠ADC=∠DCB﹣∠A=180°﹣α﹣α=180°﹣2α,∴∠ABC=180°﹣∠ADC=2α=2∠A,∴四边形ABCD是⊙O内接倍角四边形;
(2)①连接BD.
∵AD是⊙O的直径,∴∠ABD=90°.在Rt△ABD中,AD=2×5=10,sin∠A=![]() ,∴BD=8,根据勾股定理得:AB=6,设∠A=α,∴∠ADB=90°﹣α.
,∴BD=8,根据勾股定理得:AB=6,设∠A=α,∴∠ADB=90°﹣α.
由(1)知,∠ADC=180°﹣2α,∴∠BDC=90°﹣α,∴∠ADB=∠BDC,∴BC=AB=6;

②若∠ADC=60°时.
∵四边形ABCD是圆内接倍角四边形,∴∠BCD=120°或∠BAD=30°.
Ⅰ、当∠BCD=120°时,如图3,连接OA,OB,OC,OD.
∵BC=CD,∴∠BOC=∠COD,∴∠OCD=∠OCB=![]() ∠BCD=60°,∴∠CDO=60°,∴AD是⊙O的直径,(为了说明AD是直径,点O没有画在AD上)
∠BCD=60°,∴∠CDO=60°,∴AD是⊙O的直径,(为了说明AD是直径,点O没有画在AD上)
∴∠ADC+∠BCD=180°,∴BC∥AD,∴AB=CD.
∵BC=CD,∴AB=BC=CD,∴△OAB,△BOC,△COD是全等的等边三角形,∴S四边形ABCD=3S△AOB=3×![]() ×52=
×52=![]() .
.
Ⅱ、当∠BAD=30°时,如图4,连接OA,OB,OC,OD.
∵四边形ABCD是圆内接四边形,∴∠BCD=180°﹣∠BAD=150°.
∵BC=CD,∴∠BOC=∠COD,∴∠BCO=∠DCO=![]() ∠BCD=75°,∴∠BOC=∠DOC=30°,∴∠OBA=45°,∴∠AOB=90°.
∠BCD=75°,∴∠BOC=∠DOC=30°,∴∠OBA=45°,∴∠AOB=90°.
连接AC,∴∠DAC=![]() ∠BAD=15°.
∠BAD=15°.
∵∠ADO=∠OAB﹣∠BAD=15°,∴∠DAC=∠ADO,∴OD∥AC,∴S△OAD=S△OCD.
过点C作CH⊥OB于H.
在Rt△OCH中,CH=![]() OC=
OC=![]() ,∴S四边形ABCD=S△COD+S△BOC+S△AOB﹣S△AOD=S△BOC+S△AOB=
,∴S四边形ABCD=S△COD+S△BOC+S△AOB﹣S△AOD=S△BOC+S△AOB=![]() ×5+
×5+![]() ×5×5=
×5×5=![]() .
.
故答案为:![]() 或
或![]() ;
;

(3)延长DC,AB交于点E.
∵四边形ABCD是⊙O的内接四边形,∴∠BCE=∠A=![]() ∠ABC.
∠ABC.
∵∠ABC=∠BCE+∠A,∴∠E=∠BCE=∠A,∴BE=BC=b,DE=DA=b,∴CE=d﹣c.
∵∠BCE=∠A,∠E=∠E,∴△EBC∽△EDA,∴![]() ,∴
,∴![]() ,∴d2﹣b2=ab+cd.
,∴d2﹣b2=ab+cd.