题目内容
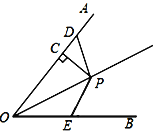
【题目】如图,P为∠AOB的平分线上一点,PC⊥OA于点C,D为OA上一点,E为OB上一点,∠ODP=180°-∠OEP.
(1)求证:PD=PE.
(2)若OC=6,求OD+OE的值.
【答案】(1)证明见解析;(2)12.
【解析】
(1)证明:作PH⊥OB于H点,根据角平分线的性质可得PH=PC,利用角角边定理可证△PDC≌△PEH,继而可得PD=PE;
(2)根据AAS就可以得出△CDP≌△EHP,从而得到CD=EH,进而得出DO+EO=12cm.
证明:作PH⊥OB于H点,
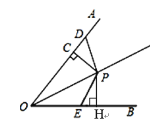
因为P为∠AOB的平分线上一点,PC⊥OA于点C,PH⊥OB于H点,
所以PH=PC,
因为∠ODP=180°-∠OEP,∠ PEH=180°-∠OEP,
所以∠ODP=∠ PEH,
所以∠PDC=∠ PEH,
在![]() 和
和![]() 中,
中,
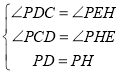
所以△PDC≌△PEH
所以PD=PE;
(2)由△PDC≌△PEH得,CD=EH,
∵DO+EO=DC+CO+EO,
∴DO+EO=EH+EO+CO,
∴DO+EO=HO+CO,
∴DO+EO=2CO,
∵CO=6cm,
∴DO+EO=12cm.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目