题目内容
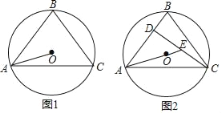
【题目】如图1,⊙O是△ABC的外接圆,连接AO,若∠BAC+∠OAB=90°.
(1)求证:![]()
(2)如图2,作CD⊥AB交于D,AO的延长线交CD于E,若AO=3,AE=4,求线段AC的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)连BO并延长BO交AC于T.只要证明BT⊥AC,利用垂径定理即可解决问题;
(2)延长AO并交⊙O于F,连接CF.在Rt△AFC中,求出CF,AF即可解决问题.
(1)证明:连BO并延长BO交AC于T.
∵ AO=BO,
∴∠ OAB=∠ OBA,
又∵ ∠ BAC+∠ OAB=90°,
∴ ∠ BAC+∠ OBA=90°,
∴ ∠ BTA=90°,
∴ BT⊥AC,
∴ ![]() .
.
(2)延长AO并交![]() O 于F,连接CF.
O 于F,连接CF.
∵ CD⊥ AB于D,
∴ ∠ CDA=90°,
∴ ∠ OAB+∠ A ED=90°,
∵ ∠ OAB+∠ BAC=90°,
∴ ∠ AED=∠ BAC=∠ FEC,
∵ AF为⊙ O直径,
∴ ∠ ACF=90°,
同理:∠ FCE=∠ BAC,
∴ ∠ FEC= ∠ FCE,
∴FE=FC,
∵AO=3,AE=4,
∴OE=1,FE=FC=2,
在Rt△FCA中
∴ AC=![]() =4
=4![]()

练习册系列答案
相关题目