��Ŀ����
��ͼ��ʾ��ֱ������OABC�Ķ���A��C�ֱ���y����������x�Ḻ�����ϣ� ����B��C��ֱ��l����ֱ��lƽ�ƣ�ƽ�ƺ��ֱ��l��x�ύ�ڵ�D����y�ύ�ڵ�E����AB=2��BC=2
����B��C��ֱ��l����ֱ��lƽ�ƣ�ƽ�ƺ��ֱ��l��x�ύ�ڵ�D����y�ύ�ڵ�E����AB=2��BC=2| 5 |
��1����ֱ������OABC�������ֱ��BC�Ľ���ʽ��
��2����ֱ��l���������ƽ��ʱ������l��ֱ��BC�غϣ�����ֱ��AB���Ƿ���ڵ�P��ʹ��PDEΪ����ֱ�������Σ������ڣ���ֱ��д���������������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
��������1���ȹ�B��BF��x�ύx����F����õ���OF=AB=2����ֱ��������BFC�������CF��OC=CF+OF���Ӷ����ֱ������OABC������������ó�B��C��������꣮�ɵ�бʽy=kx+b����B��C�������������k��b�������ֱ��BC�Ľ���ʽ��
��2����ֱ��l���������ƽ��ʱ������l��ֱ��BC�غϣ�����ֱ��AB���Ƿ���ڵ�P��ʹ��PDEΪ����ֱ�������εĵ����ȷ�������궼Ϊ4��������ȵ�ֱ�DZ�ȷ�������꣮
��2����ֱ��l���������ƽ��ʱ������l��ֱ��BC�غϣ�����ֱ��AB���Ƿ���ڵ�P��ʹ��PDEΪ����ֱ�������εĵ����ȷ�������궼Ϊ4��������ȵ�ֱ�DZ�ȷ�������꣮
����⣺��1����B��BF��x����F���ã�OF=AB=2��BF=OA=4�ҵ�ֱ��������BFC��
���Ը��ݹ��ɶ����ã�CF2=BC2-BF2=(2
)2-42=4��
��CF=2��OC=CF+OF=2+2=4��
����ֱ������OABC�����Ϊ����4+2����4��2=12��
����֪�ͼ����B��C���������ֱ�Ϊ����-2��4������-4��0����
��ֱ��BC�Ľ���ʽΪy=kx+b����ã�
4=-2k+b ��
0=-4k+b ��
�ɢ٢ڵ�k=2��b=8��
����ֱ��BC�Ľ���ʽΪ��y=2x+8��
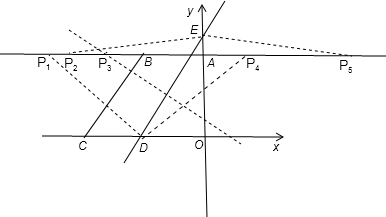
��2�����ڣ��������������ĵ�P������ֱ�Ϊ��
P1��-12��4����P2��-8��4����P3��-
��4����P4��4��4����P5��8��4����
���Ը��ݹ��ɶ����ã�CF2=BC2-BF2=(2
| 5 |
��CF=2��OC=CF+OF=2+2=4��
����ֱ������OABC�����Ϊ����4+2����4��2=12��
����֪�ͼ����B��C���������ֱ�Ϊ����-2��4������-4��0����
��ֱ��BC�Ľ���ʽΪy=kx+b����ã�
4=-2k+b ��
0=-4k+b ��
�ɢ٢ڵ�k=2��b=8��
����ֱ��BC�Ľ���ʽΪ��y=2x+8��

��2�����ڣ��������������ĵ�P������ֱ�Ϊ��
P1��-12��4����P2��-8��4����P3��-
| 8 |
| 3 |
���������⿼���֪ʶ����һ�κ�����Ӧ�ü�ֱ�������ε�����Ӧ�ã���ؼ���ͨ����ֱ��������ȷ�����������⣮

��ϰ��ϵ�д�
�����Ŀ
 3����ͼ��ʾ��ֱ������ABCD�У�AD��BC����A=90�㣬��ADC=135�㣬CD�Ĵ�ֱƽ���߽�BC��N����AB�ӳ�����F������ΪM����֤��AD=BF��
3����ͼ��ʾ��ֱ������ABCD�У�AD��BC����A=90�㣬��ADC=135�㣬CD�Ĵ�ֱƽ���߽�BC��N����AB�ӳ�����F������ΪM����֤��AD=BF�� ��2013•������һģ����һ��ֱ��������ֽƬ����ֱ�DZ��ϸ�ȡһ�㣬�ֱ���б���е��������������ȥ���������Σ�ʣ�µIJ�������ͼ��ʾ��ֱ�����Σ��������߳��ֱ�Ϊ2��4��3����ԭֱ��������ֽƬ�������
��2013•������һģ����һ��ֱ��������ֽƬ����ֱ�DZ��ϸ�ȡһ�㣬�ֱ���б���е��������������ȥ���������Σ�ʣ�µIJ�������ͼ��ʾ��ֱ�����Σ��������߳��ֱ�Ϊ2��4��3����ԭֱ��������ֽƬ������� ��2013•�˴�ģ�⣩С����һ��ֱ��������ֽƬ����ֱ�DZ��ϸ�ȡһ�㣬�ֱ���б���е��������������ȥ���������Σ�ʣ�µIJ�������ͼ��ʾ��ֱ�����Σ��������߳��ֱ�Ϊ4��8��6����ԭֱ��������ֽƬ��б�߳���
��2013•�˴�ģ�⣩С����һ��ֱ��������ֽƬ����ֱ�DZ��ϸ�ȡһ�㣬�ֱ���б���е��������������ȥ���������Σ�ʣ�µIJ�������ͼ��ʾ��ֱ�����Σ��������߳��ֱ�Ϊ4��8��6����ԭֱ��������ֽƬ��б�߳��� ����ͼ��ʾ��ֱ��������ֱ�DZ�AB��תһ�ܣ����ü����������ͼ�ǣ�������
����ͼ��ʾ��ֱ��������ֱ�DZ�AB��תһ�ܣ����ü����������ͼ�ǣ�������