题目内容
【题目】如图,在四边形ABCD中,AC平分∠DAB,CE⊥AB于E.
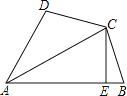
(1)若AB=AD+2BE,求证:BC=DC;
(2)若∠B=60°,AC=7,AD=6, ![]() ,求AB的长.
,求AB的长.
【答案】(1)证明见解析;(2)8.
【解析】试题分析:(1)在AB上取点F,使得EF=BE,然后根据已知条件可以推出△AFC≌△ADC,再根据全等三角形的性质即可证明结论;
(2)根据三角形ADC的面积为![]() 和AC=7,AD=6可以求出∠DAC的正弦值,而AC平分∠DAB,由此可以利用三角函数求出CE,再利用勾股定理即可求出AE、BE,最后求出AB.
和AC=7,AD=6可以求出∠DAC的正弦值,而AC平分∠DAB,由此可以利用三角函数求出CE,再利用勾股定理即可求出AE、BE,最后求出AB.
试题解析:(1)证明:如图,在AB上取点F,使得EF=BE,

∵CE⊥AB,
∴FC=BC,
∵AB=AD+2BE,而AB=AF+2BE,
∴AD=AF.
在△AFC和△ADC中,
AD=AF,∠CAF=∠CAD,AC=AC,
∴△AFC≌△ADC.
∴DC=FC.
∴BC=DC.
(2)在△ADC中,∵S△ADC=![]() ×6×7sin∠DAC=
×6×7sin∠DAC=![]() ,
,
∴sin∠DAC=![]() ,而AC平分∠DAB.
,而AC平分∠DAB.
∴![]() =
=![]() .
.
∴CE=![]() .
.
∴AE=![]() .
.
∴BE=![]() .
.
∴AB=AE+EB=8.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目