题目内容
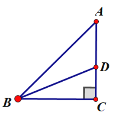
【题目】如图，在△ABC中，AC=BC，∠ACB=90°，BD平分∠ABC交AC于点D，BD=6，则△ABD的面积为__________ .
【答案】9
【解析】
过点D作DE⊥AB，交AB于点E，设DE=x，利用角平分线的性质和等腰三角形的判定可得DE=DC=AE，利用勾股定理求出AB和x的关系，再利用勾股定理和BD=6列出方程求出x2，最后代入到面积公式即可.
过点D作DE⊥AB，交AB于点E，设DE=x，
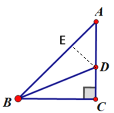
∵AC=BC，∠ACB=90°
∴∠ABC=∠A=45°
∵BD平分∠ABC，DE⊥AB，DC⊥BC
∴DE=DC，且△AED为等腰直角三角形
∴DE=DC=AE=x
∴AD=
x
∴BC=AC=AD+DC=
x
在Rt△ABC中
AB=BC=
x
在Rt△BCD中
BC2＋DC2=BD2
即：（x＋x）2＋x2=62
解得x2=18－9
∴△ABD的面积=
DE·AB
=x·x
= x2
=9
故答案为：9
练习册系列答案
相关题目
