题目内容
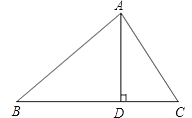
【题目】拼图填空:剪裁出若干个大小.形状完全相同的直角三角形,三边长分别记为a.b.c,如图①.





(1)拼图一:分别用4张直角三角形纸片,拼成如图②③的形状,观察图②③可发现,图②中两个小正方形的面积之和 (填“大于”.“小于”或“等于”)图③中小正方形的面积,用关系式表示为 .
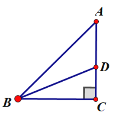
(2)拼图二:用4张直角三角形纸片拼成如图④的形状,观察图形可以发现,图中共有 个正方形,它们的面积之间的关系是 ,用关系式表示为 .
(3)拼图三:用8个直角三角形纸片拼成如图⑤的形状,图中3个正方形的面积之间的关系是 ,用关系式表示 .
【答案】(1)等于,a2+b2=c2;(2)两个小正方形面积等于大正方形面积,a2+b2=c2;(3)三个正方形的面积差相等,(b+a)2-c2=c2-(b-a)2.
【解析】
(1)利用两图形都是两个小正方形的面积之和等于大正方形减去4个直角三角形得出,即可得出面积关系,利用直角三角形各边长度得出即可;
(2)利用图形结合直角三角形面积,可以得出两个小正方形面积相加等于大正方形面积,进而得出关系时即可;
(3)利用图形可以得出图中3个正方形的面积之间的关系为三个正方形的面积差相等,进而得出关系时即可.
解:(1)∵观察图②③可发现,图②中两个小正方形的面积之和与图③中小正方形的面积,都是两个小正方形的面积之和等于大正方形减去4个直角三角形得出,
∴图②中两个小正方形的面积之和等于图③中小正方形的面积,
∵图②中两个小正方形的面积之和为(a+b)2-2ab=a2+b2,图③中小正方形的面积为:c2,
故a2+b2=c2;
故答案为:等于,a2+b2=c2;
(2)根据图形可以得出去掉大正方形与两小正方形重叠部分,正好是4个直角三角形的面积,
故图中3个正方形的面积之间的关系是:两个小正方形面积等于大正方形面积,
用关系式表示为:a2+b2=c2;
故答案为:两个小正方形面积等于大正方形面积,a2+b2=c2;
(3)利用图形可以得出:大正方形面积-中正方形面积=中正方形面积-小正方形面积,即图中3个正方形的面积之间的关系是:三个正方形的面积差相等;
用关系式表示为:(b+a)2-c2=c2-(b-a)2.
故答案为:三个正方形的面积差相等,(b+a)2-c2=c2-(b-a)2.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案