Question

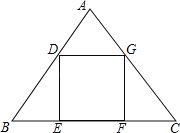
【题目】如图，正方形DEFG的边EF在△ABC的边BC上，顶点D、G分别在边AB、AC上，已知BC＝6，△ABC的面积为9，则正方形DEFG的面积为_____．

Answer 1

【答案】4

【解析】

由DG∥BC得△ADG∽△ABC，利用相似三角形对应边上高的比等于相似比，列方程求解．

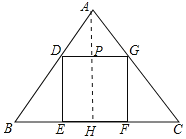
解：作AH⊥BC于H，交DG于P，如图所示：

∵△ABC的面积＝BCAH＝9，BC＝6，

∴AH＝3，

设正方形DEFG的边长为x．

由正方形DEFG得，DG∥EF，即DG∥BC，

∵AH⊥BC，

∴AP⊥DG．

由DG∥BC得△ADG∽△ABC

∴．

∵PH⊥BC，DE⊥BC

∴PH＝ED，AP＝AH﹣PH，

即，

由BC＝6，AH＝3，DE＝DG＝x，

得，

解得x＝2．

故正方形DEFG的面积＝22＝4；

故答案为：4．