题目内容
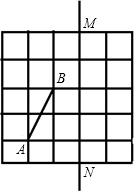在5×5正方形网格中，有线段AB和直线MN．
（1）在MN上找一点C，使△ABC的周长最小；
（2）在网格中作出点P，使△ABP以AB为腰的等腰三角形，且点P要在格点上，则这样的点P有多少个？
解：（1）
作B关于直线MN的对称点D，连接AD交MN于C，
则此时△ABC的周长最小．
（2）如图所示
当BA=BP时，符合条件的点有：Q、Z、E、L、F、W共6个，
当AB=AP时，符合条件的点有：T、G、H共3个
∴这样的点P有9个．
分析：（1）作出B关于MN的对称点D，连接AD即可得到答案；
（2）根据要求得到①当BA=BP时，符合条件的点有6个，②当AB=AP时，符合条件的点有3个，即可求出答案．
点评：本题主要考查对等腰三角形的判定和性质，勾股定理，轴对称-最短路线问题等知识点的理解和掌握，能根据题意画出图形式解此题的关键．
作B关于直线MN的对称点D，连接AD交MN于C，
则此时△ABC的周长最小．
（2）如图所示
当BA=BP时，符合条件的点有：Q、Z、E、L、F、W共6个，
当AB=AP时，符合条件的点有：T、G、H共3个
∴这样的点P有9个．
分析：（1）作出B关于MN的对称点D，连接AD即可得到答案；
（2）根据要求得到①当BA=BP时，符合条件的点有6个，②当AB=AP时，符合条件的点有3个，即可求出答案．
点评：本题主要考查对等腰三角形的判定和性质，勾股定理，轴对称-最短路线问题等知识点的理解和掌握，能根据题意画出图形式解此题的关键．
练习册系列答案
相关题目
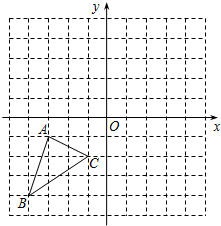19、如图，在正方形网格中，△ABC的三个顶点都在格点上，结合所给的平面直角坐标系解答下列问题：
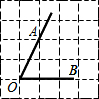如图，∠AOB放置在正方形网格中，则cos∠AOB的值为（ ）
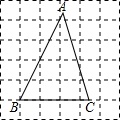在正方形网格中，△ABC在网格中的位置如图，则cosB的值为（ ）
