题目内容
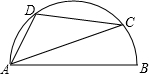
已知AB是半圆的直径，BC切半圆于B点，BC=
=r，AC交半圆于D点，DE⊥AB于E，则DE的长为（ ）
| AB |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析：解答此题的关键是连接BD，则AD⊥DB，利用BC切半圆于B点，BC=
=r，求出AD，再利用AC交半圆于D点，DE⊥AB于E，求出DE的长．
| AB |
| 2 |
解答：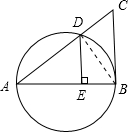
解：如图，连接BD，则AD⊥DB．
∵BC切半圆于B，AB为直径，
∴CB⊥AB，
∵BC=r，AB=2r，
∴AC=
r．
∵BC2=CD•CA，
∴CD=
r，AD=AC-CD=
r，
又DE⊥AB，
∴AC•BD=AB•BC，得BD=
r．
∵AB•DE=AD•BD，
∴DE=
r．
故选D．
解：如图，连接BD，则AD⊥DB．∵BC切半圆于B，AB为直径，
∴CB⊥AB，
∵BC=r，AB=2r，
∴AC=
| 5 |
∵BC2=CD•CA，
∴CD=
| ||
| 5 |
4
| ||
| 5 |
又DE⊥AB，
∴AC•BD=AB•BC，得BD=
2
| ||
| 5 |
∵AB•DE=AD•BD，
∴DE=
| 4 |
| 5 |
故选D．
点评：此题考查学生对相似三角形的判定与性质，圆周角定理的理解与掌握．
练习册系列答案
相关题目
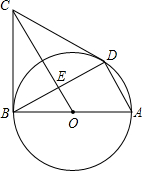有一点D使∠ABD=30°，BD的中点为E，连接OE并延长OE与BC交于点C，连接CD．
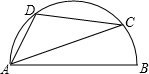如图，已知AB是半圆的直径，∠BAC=20°，D是
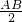=r，AC交半圆于D点，DE⊥AB于E，则DE的长为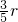
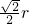
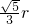
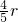
如图，已知AB是半圆的直径，∠BAC=20°，D是
上任意一点，则∠D的度数是