题目内容
如图,已知AB是⊙O的直径,且AB为6,过B点作⊙O的切线CB与⊙O相切于点B,在半圆AB上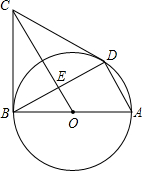 有一点D使∠ABD=30°,BD的中点为E,连接OE并延长OE与BC交于点C,连接CD.
有一点D使∠ABD=30°,BD的中点为E,连接OE并延长OE与BC交于点C,连接CD.(1)求证:CD是⊙O的切线.
(2)四边形ABCD的周长是多少?
分析:(1)连接OD,根据OB=OD,E是BD的中点可知OC是线段BD的垂直平分线,再根据全等三角形的判定定理可判定出△OBC≌△ODC,再由BC是⊙O的切线可得出∠OBC=90°,由全等三角形的性质可得出∠ODC=90°,即CD是⊙O的切线;
(2)先根据BC是⊙O的垂线及∠ABD的度数可求出∠DBC的度数,再由BC=CD可知△BDC是等边三角形,故BC=BD=CD,再由直角三角形的性质可得出AD、BD的长,进而可求出答案.
(2)先根据BC是⊙O的垂线及∠ABD的度数可求出∠DBC的度数,再由BC=CD可知△BDC是等边三角形,故BC=BD=CD,再由直角三角形的性质可得出AD、BD的长,进而可求出答案.
解答: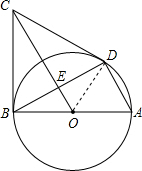 (1)证明:连接OD,
(1)证明:连接OD,
∵OE是BD的中点且BO=DO,
∴OE⊥BD,
∴CE⊥BD,
∵BE=DE,
∴BC=DC,
∵OB=OD,OC=OC,
∴△OBC≌△ODC,
∵BC是⊙O的切线,
∴∠OBC=90°,
∴∠ODC=90°,
∴CD是⊙O的切线;
(2)∵BC是⊙O的切线,
∴∠OBC=90°,
∵∠ABD=30°,
∴∠DBC=60°,
∵BC=CD,
∴∠DBC=∠BDC=60°,
∴△BCD是等边三角形,
∴BC=BD=CD,
∵AB是直径,
∴∠ADB=90°,
∵∠ABD=30°,AB=6,
∴AD=
AB=
×=3,BD=
=
=3
,
∴四边形ABCD的周长为:3
+3
+3+6=9+6
.
 (1)证明:连接OD,
(1)证明:连接OD,∵OE是BD的中点且BO=DO,
∴OE⊥BD,
∴CE⊥BD,
∵BE=DE,
∴BC=DC,
∵OB=OD,OC=OC,
∴△OBC≌△ODC,
∵BC是⊙O的切线,
∴∠OBC=90°,
∴∠ODC=90°,
∴CD是⊙O的切线;
(2)∵BC是⊙O的切线,
∴∠OBC=90°,
∵∠ABD=30°,
∴∠DBC=60°,
∵BC=CD,
∴∠DBC=∠BDC=60°,
∴△BCD是等边三角形,
∴BC=BD=CD,
∵AB是直径,
∴∠ADB=90°,
∵∠ABD=30°,AB=6,
∴AD=
| 1 |
| 2 |
| 1 |
| 2 |
| AB2-AD2 |
| 62-32 |
| 3 |
∴四边形ABCD的周长为:3
| 3 |
| 3 |
| 3 |
点评:本题考查的是切线的判定与性质、圆周角定理及线段垂直平分线的性质、等边三角形的判定与性质,涉及面较广,根据题意作出辅助线是解答此题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
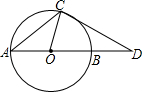 如图,已知AB是⊙O的直径,AC是弦,D为AB延长线上一点,DC=AC,∠ACD=120°,BD=10.
如图,已知AB是⊙O的直径,AC是弦,D为AB延长线上一点,DC=AC,∠ACD=120°,BD=10.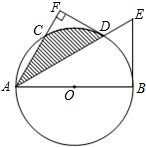 如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.
如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.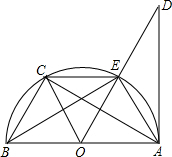 (2013•泰安)如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是
(2013•泰安)如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是
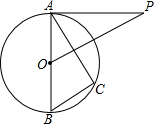 如图,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC.
如图,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC.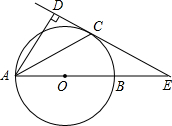 如图,已知AB是圆O的直径,∠DAB的平分线AC交圆O与点C,作CD⊥AD,垂足为点D,直线CD与AB的延长线交于点E.
如图,已知AB是圆O的直径,∠DAB的平分线AC交圆O与点C,作CD⊥AD,垂足为点D,直线CD与AB的延长线交于点E.