题目内容
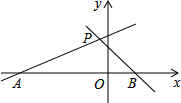 已知两条直线y=(
已知两条直线y=(| 1 | 2 |
(1)点P的坐标;
(2)S△APB的面积.
分析:(1)联立两个解析式,组成方程组,再解方程即可得到P点坐标;
(2)分别利用函数解析式计算出A、B两点的坐标,在求△APB的面积即可.
(2)分别利用函数解析式计算出A、B两点的坐标,在求△APB的面积即可.
解答:解:(1)
,解得
,
故P(-1,2);
(2)∵函数y=(
)x+2.5中,当y=0时,x=-5,
∴A(-5,0),
∵函数y=-x+1中,当y=0时,x=1,
∴B(1,0),
∴S△APB=
×6×2=6.
|
|
故P(-1,2);
(2)∵函数y=(
| 1 |
| 2 |
∴A(-5,0),
∵函数y=-x+1中,当y=0时,x=1,
∴B(1,0),
∴S△APB=
| 1 |
| 2 |
点评:此题主要考查了两函数图象交点问题,关键是两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
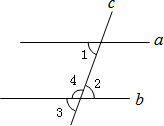 如图,已知两条直线a,b被第三条直线c所截,若∠1=∠2,求证:∠1=∠3,∠1+∠4=180°.
如图,已知两条直线a,b被第三条直线c所截,若∠1=∠2,求证:∠1=∠3,∠1+∠4=180°. 已知两条直线y1=2x-4和y2=5-x.
已知两条直线y1=2x-4和y2=5-x.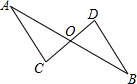 如图,已知两条直线AB,CD相交于点O,且CO=DO,AC∥BD,求证:△AOC≌△BOD.
如图,已知两条直线AB,CD相交于点O,且CO=DO,AC∥BD,求证:△AOC≌△BOD.