Question

已知两条直线y=

n

n+1

x+

2

n+1

和y=-

n

n+1

x+

2

n+1

（n为正整数），设它们与x轴围成的图形面积为S_n（n=1，2，…，2010），求S₁+S₂+…+S₂₀₁₀的值．

Answer 1

分析：观察两条直线的解析式发现，两直线关于y轴对称，且在y轴上交于一点，与x轴的交点关于原点对称，根据题意画出图形，表示出两条直线与x轴围成的面积S_n，利用拆项法把所求式子的每一项变形，抵消后即可求出的值．

解答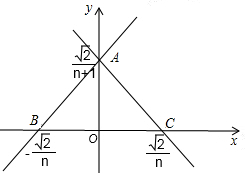：解：令x=0，由直线y=

n

n+1

x+

2

n+1

，解得y=

2

n+1

，令y=0，解得x=-

2

n

，
所以该直线与x轴的交点坐标为（-

2

n

，0），与y轴的交点坐标为（0，

2

n+1

）；
令x=0，由直线y=-

n

n+1

x+

2

n+1

，解得y=

2

n+1

，令y=0，解得x=

2

n

，
所以该直线与x轴的交点坐标为（

2

n

，0），与y轴的交点坐标为（0，

2

n+1

），
根据题意画出图形，如图所示：

由图形可知：△ABC的面积为两直线与x轴围成图形的面积S_n，
所以S_n=S_△ABC=

1

2

|BC|•|OA|=

1

2

×

2 2

n

×

2

n+1

=

2

n(n+1)

=2（

1

n

-

1

n+1

），
则S₁+S₂+…+S₂₀₁₀=2（1-

1

2

+

1

2

-

1

3

+…+

1

2010

-

1

2011

）=2（1-

1

2011

）=

4020

2011

．

点评：此题考查了一次函数与坐标轴的交点求法，以及求一组数的和的方法．借助图形得到所求的面积即为三角形ABC的面积，表示出S_n是解本题的关键，同时注意利用“拆项法”即灵活利用

1

n(n+1)

=

1

n

-

1

n+1

，把两直线与x轴围成的面积S_n进行变形．