题目内容
在□ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F。
小题1:在图1中证明
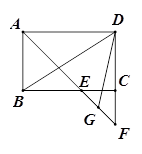
小题2:若 ,G是EF的中点(如图2),直接写出∠BDG的度数;
,G是EF的中点(如图2),直接写出∠BDG的度数;
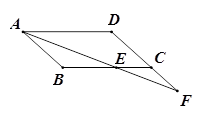
小题3:若 ,FG∥CE,
,FG∥CE, ,分别连结DB、DG(如图3),求∠BDG的度数。
,分别连结DB、DG(如图3),求∠BDG的度数。
小题1:在图1中证明

小题2:若
 ,G是EF的中点(如图2),直接写出∠BDG的度数;
,G是EF的中点(如图2),直接写出∠BDG的度数;小题3:若
 ,FG∥CE,
,FG∥CE, ,分别连结DB、DG(如图3),求∠BDG的度数。
,分别连结DB、DG(如图3),求∠BDG的度数。小题1:证明:如图1.

∵
 平分
平分
∴
 .
.∵四边形
 是平行四边形,
是平行四边形,∴
 .
.∴
 .
.∴
 .
.∴
 .(2分)
.(2分)小题2:
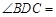
 .(3分)
.(3分)小题3:解:分别连结
 、
、 、
、 (如图2).
(如图2).
∵

∴

∵
 且
且
∴四边形
 是平行四边形.
是平行四边形.由⑴得

∴
 是菱形.
是菱形.∴
 .
.∴
 是等边三角形.
是等边三角形.∴
 ①
① .
.∴
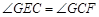 .
.∴
 . ②
. ②由
 及
及 平分
平分 可得
可得 .
.∴
 .
.在
 中,
中, .
.∴
 . ③
. ③由①②③得
 .
.∴

 .
.∴
 .
.
∴
 .(5分)
.(5分)(1)根据AF平分∠BAD,可得∠BAF=∠DAF,利用四边形ABCD是平行四边形,求证∠CEF=∠F.即可
(2)根据∠ABC=90°,G是EF的中点可直接求得.
(3)分别连接GB、GC,求证四边形CEGF是平行四边形,再求证△ECG是等边三角形.由AD∥BC及AF平分∠BAD可得∠BAE=∠AEB,求证△BEG≌△DCG,然后即可求得答案。

(2)根据∠ABC=90°,G是EF的中点可直接求得.
(3)分别连接GB、GC,求证四边形CEGF是平行四边形,再求证△ECG是等边三角形.由AD∥BC及AF平分∠BAD可得∠BAE=∠AEB,求证△BEG≌△DCG,然后即可求得答案。




练习册系列答案
相关题目


 是平面上不共线的三点,那么,以
是平面上不共线的三点,那么,以


 -
-
 -
-
 -4.
-4. -
- .
.