题目内容
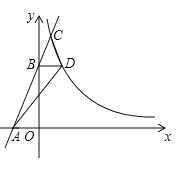
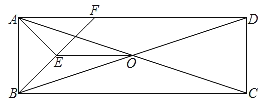
【题目】如图,在矩形ABCD中,对角线AC与BD相交于点O,F为DA上一点,连接BF,E为BF中点,CD=6,sin∠ADB=![]() ,若△AEF的周长为18,则S△BOE=_____.
,若△AEF的周长为18,则S△BOE=_____.
【答案】![]()
【解析】
根据题意求出AD=18,设AF=![]() ,则BF=
,则BF=![]() ,在Rt△ABF中,利用勾股定理可求得
,在Rt△ABF中,利用勾股定理可求得![]() ,求出DF=10,可求出S△BDF,由三角形中位线定理可求出答案.
,求出DF=10,可求出S△BDF,由三角形中位线定理可求出答案.
∵四边形ABCD是矩形,
∴AB=CD=6,∠BAD=90°,OB=OD,
∵sin∠ADB=![]() ,
,
∴![]() ,
,
∴BD![]() ,
,
∴![]() ,
,
∵E为BF中点,
∴AE=BE=EF,
∵△AEF的周长为18,
∴AE+EF+AF=BE+EF+AF=BF+AF=18,
设AF=![]() ,则BF=
,则BF=![]() ,
,
在Rt△ABF中,AB2+AF2=BF2,
∴62+![]() 2=(
2=(![]() )2,
)2,
解得:![]() ,
,
∴DF=18-8=10.
∵E为BF中点,O为BD的中点,
∴OE∥DF,OE=![]() DF,
DF,
∴△BOE∽△BDF,
∴![]() ,
,
∵![]() DFAB=
DFAB=![]() ×6×10=30,
×6×10=30,
∴S△BOE=![]() .
.
故答案为:![]() .
.

【题目】市少年宫为小学生开设了绘画、音乐、舞蹈和跆拳道四类兴趣班,为了解学生对这四类兴趣班的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制了一幅不完整的统计表

兴趣班 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
| |
合计 |
|
请你根据统计表中提供的信息回答下列问题:
(1)统计表中的![]() _____,
_____,![]() ;
;
(2)根据调查结果,请你估计该市![]() 名小学生中最喜欢“绘画”兴趣班的人数;
名小学生中最喜欢“绘画”兴趣班的人数;
(3)王强和李昊选择参加兴趣班,若王强从![]() 三类兴趣班中随机选取一类,李吴从
三类兴趣班中随机选取一类,李吴从![]() 三类兴趣班中随机选取一类,请用画树状图或列表格的方法,求两人恰好选中同一类兴趣班的概率.
三类兴趣班中随机选取一类,请用画树状图或列表格的方法,求两人恰好选中同一类兴趣班的概率.
【题目】为培养学生庭好的学习习惯,某校九年级年级组举行“整理错题集“的征集展示活动,并随机对部分学生三年“整理题集”中收集的错题数x进行了抽样调查,根据收集的数据绘制了下面不完整的统计图表.
分组 | 频数 | 频率 |
第一组(0≤x<120) | 3 | 0.15 |
第二组(120≤x<160) | 8 | a |
第三组(160≤x<200) | 7 | 0.35 |
第四组(200≤x<240) | b | 0.1 |
请你根据图表中的信息完成下列问题:
(1)频数分布表中a= ,b= ,并将统计图补充完整;
(2)如果该校九年级共有学生360人,估计整理的错题数在160或160题以上的学生有多少人?
(3)已知第一组中有两个是甲班学生,第四组中有一个是甲班学生,老师随机从这两个组中各选一名学生谈整理错题的体会,则所选两人正好都是甲班学生的概率是多少?