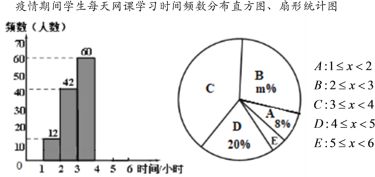
题目内容
【题目】早在古罗马时代,传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题.
将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的军营B开会,应该怎样走才能使路程最短?这个问题的答案并不难,据说海伦略加思索就解决了它.从此以后,这个被称为“将军饮马”的问题便流传至今.大数学家海伦曾用轴对称的方法巧妙地解决了这个问题.
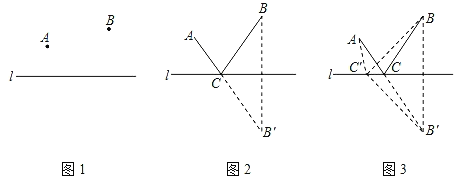
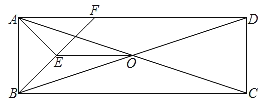
如图2,作B关于直线l的对称点B′,连结AB′与直线l交于点C,点C就是所求的位置.
证明:如图3,在直线l上另取任一点C′,连结AC′,BC′,B′C′,
∵直线l是点B,B′的对称轴,点C,C′在l上,
∴CB=CB′,C′B=C′B′,
∴AC+CB=AC+ = .
在△AC′B′中,
∵AB′<AC′+C′B′
∴AC+CB<AC′+C′B′即AC+CB最小.
本问题实际上是利用轴对称变换的思想,把A,B在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即“三角形两边之和大于第三边”的问题加以解决(其中C在AB′与l的交点上,即A、C、B′三点共线).本问题可归纳为“求定直线上一动点与直线外两定点的距离和的最小值”的问题的数学模型.
1.简单应用
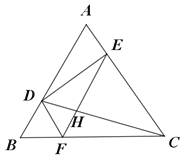
(1)如图4,在等边△ABC中,AB=6,AD⊥BC,E是AC的中点,M是AD上的一点,求EM+MC的最小值
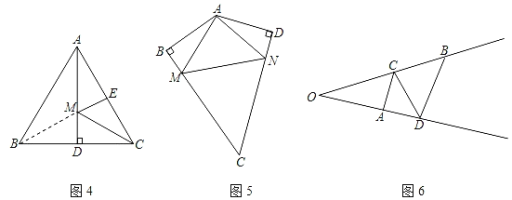
借助上面的模型,由等边三角形的轴对称性可知,B与C关于直线AD对称,连结BM,EM+MC的最小值就是线段 的长度,则EM+MC的最小值是 ;
(2)如图5,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC,CD上分别找一点M、N当△AMN周长最小时,∠AMN+∠ANM= °.
2.拓展应用
如图6,是一个港湾,港湾两岸有A、B两个码头,∠AOB=30°,OA=1千米,OB=2千米,现有一艘货船从码头A出发,根据计划,货船应先停靠OB岸C处装货,再停靠OA岸D处装货,最后到达码头B.怎样安排两岸的装货地点,使货船行驶的水路最短?请画出最短路线并求出最短路程.
【答案】C′B;AB′;简单应用:(1)BE;3![]() ;(2)100;拓展应用:作图见解析,货船行驶的水路最短路程为
;(2)100;拓展应用:作图见解析,货船行驶的水路最短路程为![]() 千米
千米
【解析】
1.简单应用
(1)根据等边三角形的性质、勾股定理计算,得到答案;
(2)作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,根据等腰三角形的性质、三角形内角和定理计算;
2.拓展应用
分别作点A关于OB的对称点A′,点B关于OA的对称点B′,连接A′B′,交OB于C,交OA于D,根据轴对称的性质、勾股定理计算,得到答案.
解:AC+CB=AC+C′B=AB′,
故答案为:C′B;AB′;
1.简单应用
(1)由等边三角形的轴对称性可知,B与C关于直线AD对称,连结BM,
EM+MC的最小值就是线段BE的长度,
BE=![]() ,
,
则EM+MC的最小值是![]() ,
,
故答案为:BE;![]() ;
;
(2)如图5,作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,
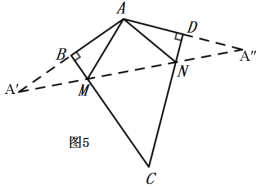
则A′A″即为△AMN的周长最小值,
∵∠DAB=130°,
∴∠A′+∠A″=50°,
∵∠A′=∠MAA′,∠NAD=∠A″,
且∠A′+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠A′+∠MAA′+∠NAD+∠A″=2(∠A′+∠A″)=2×50°=100°,
故答案为:100;
2.拓展应用
如图6,分别作点A关于OB的对称点A′,点B关于OA的对称点B′,连接A′B′,交OB于C,交OA于D,则C、D为两岸的装货地点,A′B′是货船行驶的水路最短路程,
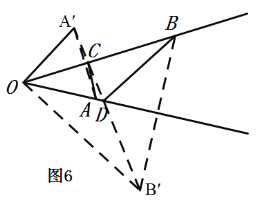
由轴对称的性质可知,OA′=OA=1,OB′=OB=2,∠BOA′=∠AOB=30°,∠AOB′=∠AOB=30°,
∴∠A′OB′=90°,
∴A′B′=![]() ,
,
答:货船行驶的水路最短路程为![]() 千米.
千米.

【题目】华联超市用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该商场购进甲、乙两种商品各多少件?
(2)该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?