Question

【题目】如图，公路PQ和公路MN交于点P，且∠NPQ=45°，公路PQ上有一所学校A，AP=80米，现有一拖拉机在公路MN上以10米∕秒的速度行驶，拖拉机行驶时周围100米以内会受到噪声的影响，请判断拖拉机在行驶过程中是否对学校会造成影响，并说明理由，如果造成影响，求出造成影响的时间.

Answer 1

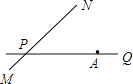
【答案】受影响的时间为12秒.

【解析】试题分析：

过点A作AB⊥DP于点B，则AB是点A到道路MN的最短距离，结合已知条件求出AB的长度为80米，由80<100可知，学校要受影响；再以点A为圆心，100米为半径作圆A交MN于点C和点D，连接AD、CD，利用已知条件求出CD的长，用CD的长度除以10，可得受影响的时间.

试题解析：

作AB⊥DP于B，则AB为A到道路的最短距离，

在Rt△APB中，∵∠NPQ=45°，

∴∠PAB=∠NPQ=45°，

∴BA=BP，

∴BA2+BP2=AP2=()2，

∴BA=BP=80，

∵80小于100，

∴有影响；

以点A为圆心，100米为半径作圆A交MN于点C和点D，连接AD、CD，

∴在Rt△ABD中，BD=（米），

∵AC=AD，AB⊥CD，

∴CB=BD=60，

∴受影响的时间为：（60×2）÷10=12秒.