题目内容
【题目】(本题8分)如图,⊙O是△ABC的外接圆,AD⊥BC于点D,直径CF⊥AB于点E,AD、FC的延长线交于点M。
(1)求证:EF=EM;
(2)若![]() ,AC=8,求sinM的值.
,AC=8,求sinM的值.

【答案】(1)答案见解析 (2)![]()
(1)证明:连AF,∵∠DCE=∠B+∠CEB=∠M+CDM而AD⊥BC于点D,CF⊥AB于点E,∴∠CEB=∠CDM∴∠B=∠M,又∵∠B=∠F,∴∠M=∠F,∴AM=AF又∵EF=EM
(2)解:连AO,∵CF为直径,AB⊥CF于点E,∴AE=BE∴CA=CB,∠B=∠BAC,而∠AOE=2∠B,∠ACD=∠B+∠BAC=2∠B∴∠ACD=∠AOE,又∵AD⊥BD,AE⊥CF,∴∠ADC=∠AEO
△ADC∽△AEO,∴![]() ,而AC=8,∴CF=2AO=12
,而AC=8,∴CF=2AO=12
∵CF为直径,∴∠CAF=90°,∴在Rt△CAF中
AF=![]() =
=![]() =4
=4![]() ,∴AM=4
,∴AM=4![]() ,易求
,易求
△OCA中AC上的高为2![]() ,用面积法求得AE=
,用面积法求得AE=![]() ,sinM=
,sinM=![]()
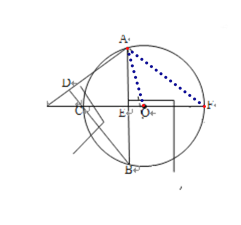
【解析】试题分析:本题考查了外角的性质,圆周角定理的推论,等腰三角形的判定与性质,垂径定理及其推论,相似三角形的判定与性质,勾股定理.
由三角形内角和得到∠B=∠M,由圆周角定理的推论可得∠B=∠F,从而∠M=∠F, △AMF是等腰三角形,由三线合一的性质可得EF=EM;
由垂径定理可得CA=CB,∠B=∠BAC,由圆周角定理的推论和外角性质可得∠ACD=∠AOE,进而证明△ADC∽△AEO,得到![]() ,求出CF的长,然后根据勾股定理求AF,面积法求AE,从而求sinM的值.
,求出CF的长,然后根据勾股定理求AF,面积法求AE,从而求sinM的值.
试题解析:
(1)证明:连AF,∵∠DCE=∠B+∠CEB=∠M+CDM而AD⊥BC于点D,CF⊥AB于点E,∴∠CEB=∠CDM∴∠B=∠M,又∵∠B=∠F,∴∠M=∠F,∴AM=AF又∵EF=EM
(2)解:连AO,∵CF为直径,AB⊥CF于点E,∴AE=BE∴CA=CB,∠B=∠BAC,而∠AOE=2∠B,∠ACD=∠B+∠BAC=2∠B∴∠ACD=∠AOE,又∵AD⊥BD,AE⊥CF,∴∠ADC=∠AEO
△ADC∽△AEO,∴![]() ,而AC=8,∴CF=2AO=12
,而AC=8,∴CF=2AO=12
∵CF为直径,∴∠CAF=90°,∴在Rt△CAF中
AF=![]() =
=![]() =4
=4![]() ,∴AM=4
,∴AM=4![]() ,易求
,易求
△OCA中AC上的高为2![]() ,用面积法求得AE=
,用面积法求得AE=![]() ,sinM=
,sinM=![]()
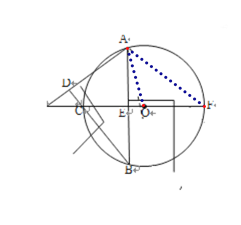

【题目】甲、乙、丙、丁四人参加训练,近期的10次百米测试平均成绩都是13.2秒,方差如表
选手 | 甲 | 乙 | 丙 | 丁 |
方差(秒2) | 0.020 | 0.019 | 0.021 | 0.022 |
则这四人中发挥最稳定的是( )
A.甲
B.乙
C.丙
D.丁