题目内容
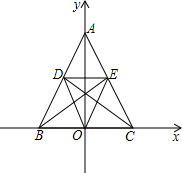 如图,在直角坐标系中,点B坐标为(-4,0),点C与点B关于原点O对称,点A为y轴上一动点,其坐标为(0,k),BE,CD分别为△ABC中AC,AB边上的高,垂足分别为E,D.
如图,在直角坐标系中,点B坐标为(-4,0),点C与点B关于原点O对称,点A为y轴上一动点,其坐标为(0,k),BE,CD分别为△ABC中AC,AB边上的高,垂足分别为E,D.(1)当k=-3时,求AB的长;
(2)试说明△DOE是等腰三角形;
(3)k取何值时,△DOE是等边三角形?(直接写出k的值即可)
分析:(1)根据点B坐标为(-4,0),点C与点B关于原点O对称,点A为y轴上一动点,其坐标为(0,k),当k=-3时,求出点A的坐标,再根据勾股定理即可求出AB的长;
(2)根据C与点B关于原点O对称,求出OB=OC,再根据BE是△ABC中AC边上的高,求出OE和OD的值,从而得出OD=OE,即可得出△DOE是等腰三角形;
(3)分△ABC是锐角三角形和钝角三角形两种情况进行讨论,即可得出k的值.
(2)根据C与点B关于原点O对称,求出OB=OC,再根据BE是△ABC中AC边上的高,求出OE和OD的值,从而得出OD=OE,即可得出△DOE是等腰三角形;
(3)分△ABC是锐角三角形和钝角三角形两种情况进行讨论,即可得出k的值.
解答:解:(1)∵点B坐标为(-4,0),当k=-3时,A的坐标为(0,-3),
∴OA=3,OB=4,
∴AB=
=5;
(2)∵点C与点B关于原点O对称,
∴OB=OC,
∵BE是△ABC中AC边上的高,
∴OE=
,
同理OD=
,
∴OD=OE,
∴△DOE是等腰三角形;
(3)当△ABC是锐角三角形,点A在y轴的正半轴时,
若△ODE为等边三角形,则∠DOE=60°,
∵∠BOD=∠COE=60°,
∵OD=OB,
∴∠DBO=60°,
∴∠BAO=30°,
∴AB=2BO=8,
∴OA=
=
=4
,
∴k=4
,
当点A在y轴的负半轴时,
k=-4
,
如图: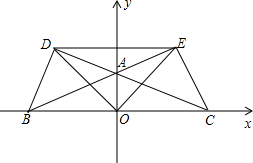 当△ABC是钝角三角形时,
当△ABC是钝角三角形时,
若△ODE为等边三角形,则∠DOE=60°,
∵∠BOD=∠COE,
∴∠COE=60°,
∵OE=OB,
∴∠OBE=∠OEB=30°,
∴AB=2AO=2|k|,
k2+42=(2k)2,
k=±
;
则k=±
或±4
.
∴OA=3,OB=4,
∴AB=
| 32+42 |
(2)∵点C与点B关于原点O对称,
∴OB=OC,
∵BE是△ABC中AC边上的高,
∴OE=
| BC |
| 2 |
同理OD=
| BC |
| 2 |
∴OD=OE,
∴△DOE是等腰三角形;
(3)当△ABC是锐角三角形,点A在y轴的正半轴时,
若△ODE为等边三角形,则∠DOE=60°,
∵∠BOD=∠COE=60°,
∵OD=OB,
∴∠DBO=60°,
∴∠BAO=30°,
∴AB=2BO=8,
∴OA=
| AB2-BO2 |
| 82-42 |
| 3 |
∴k=4
| 3 |
当点A在y轴的负半轴时,
k=-4
| 3 |
如图:
 当△ABC是钝角三角形时,
当△ABC是钝角三角形时,若△ODE为等边三角形,则∠DOE=60°,
∵∠BOD=∠COE,
∴∠COE=60°,
∵OE=OB,
∴∠OBE=∠OEB=30°,
∴AB=2AO=2|k|,
k2+42=(2k)2,
k=±
| 4 |
| 3 |
| 3 |
则k=±
| 4 |
| 3 |
| 3 |
| 3 |
点评:此题考查了等边三角形的判定,用到的知识点是坐标与图形的性质、等腰三角形的判定和勾股定理,熟练掌握有关定义和性质是本题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: