题目内容
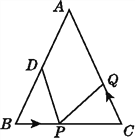
【题目】如图,在△ABC中,D为AB的中点,AD=5 cm,∠B=∠C,BC=8 cm.
(1)若点P在线段BC上以3 cm/s的速度从点B向终点C运动,同时点Q在线段CA上从点C向终点A运动.
①若点Q的速度与点P的速度相等,经过1 s后,请说明△BPD≌△CQP.
②若点Q的速度与点P的速度不等,当点Q的速度为多少时,能使△BPD≌△CPQ?
(2)若点P以3 cm/s的速度从点B向点C运动,同时点Q以5 cm/s的速度从点C向点A运动,它们都依次沿△ABC三边运动,则经过多长时间,点Q第一次在△ABC的哪条边上追上点P?
【答案】(1)说明见解析;(2)当点Q的运动速度为![]() cm/s时,能使△BPD≌△CPQ.(3)10s.
cm/s时,能使△BPD≌△CPQ.(3)10s.
【解析】试题分析:(1)①根据等腰三角形的性质得到∠B=∠C,再加上BP=CQ=3,PC=BD=5,则可判断△BPD与△CQP全等;
②设点Q的运动速度为xcm/s,则BP=3t,CQ=xt,CP=8-3t,当△BPD≌△CQP,则BP=CQ,CP=BD;然后分别建立关于t和v的方程,再解方程即可;
(2)设经过x秒后,点Q第一次追上点P,由题意得5x-3x=2×10,解方程得到点P运动的路程为3×10=30,得到此时点P在BC边上,于是得到结果.
试题解析:(1)①∵BP=3×1=3,CQ=3×1=3,
∴BP=CQ,
∵D为AB的中点,
∴BD=AD=5,
∵CP=BC-BP=5,
∴BD=CP,
在△BPD与△CQP中,
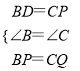 ,
,
∴△BPD≌△CQP;
②设点Q运动时间为t秒,运动速度为vcm/s,
∵△BPD≌CPQ,
∴BP=CP=4,CQ=5,
∴t=![]() ,
,
∴v=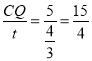 ;
;
(2)设经过x秒后,点Q第一次追上点P,由题意得5x-3x=2×10,
解得:x=10,
∴点P运动的路程为3×10=30,
∵30=28+2,
∴此时点P在BC边上,
∴经过10秒,点Q第一次在BC边上追上点P.

 应用题作业本系列答案
应用题作业本系列答案