题目内容
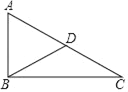
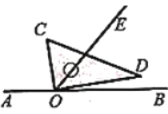
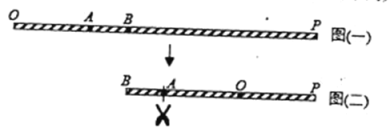
【题目】如图(一),![]() 为一条拉直的细线,
为一条拉直的细线,![]() 两点在
两点在![]() 上,且
上,且![]() . 若先固定
. 若先固定![]() 点,将
点,将![]() 折向
折向![]() ,使得
,使得![]() 重迭在BP上,如图(二);再从图(二)的
重迭在BP上,如图(二);再从图(二)的![]() 点及与
点及与![]() 点重迭处一起剪开,使得细线分成三段,则此三段细线由小到大的长度比为( )
点重迭处一起剪开,使得细线分成三段,则此三段细线由小到大的长度比为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
根据题意可以设出线段OP的长度,从而根据比值可以得到图一中各线段的长,根据题意可以求出折叠后,再剪开各线段的长度,从而可以求得三段细线由小到大的长度比,本题得以解决.
设OP的长度为8a,
∵OA:AP=1:3,OB:BP=3:5,
∴OA=2a,AP=6a,OB=3a,BP=5a,
又∵先固定B点,将OB折向BP,使得OB重叠在BP上,
如图(二),再从图(二) 的A点及与A点重叠处一起剪开,使得细线分成三段,
∴这三段从小到大的长度分别是:2a、2a、4a,
∴此三段细线由小到大的长度比为:2a:2a:4a=1:1:2.
故选B.

练习册系列答案
相关题目