Question

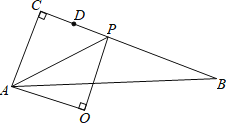
【题目】如图，在∠△ACB和△DCE中，AC＝BC，CD＝CE，∠ACB＝∠DCE＝90°，连接AE、BD交于点O，AE与DC交于点M，BD与AC交于点N．试判断AE、BD之间的关系，并说明理由．

Answer 1

【答案】AE＝BD且AE⊥BD．理由见解析.

【解析】

根据全等三角形的性质即可求证△ACE≌△BCD，从而可知AE=BD，然后再证明∠DOM＝∠ECM＝90°，即可解答.

AE＝BD且AE⊥BD．理由如下：

∵∠ACB＝∠DCE，

∴∠ACB+∠DCA＝∠DCE+∠DCA，

即∠DCB＝∠ACE，

∵AC＝BC，CD＝CE，

∴△ACE≌△BCD（SAS），

∴AE＝BD，∠CEA＝∠BDC，

∵∠CME＝∠DMO，

∴∠DOM＝∠ECM＝90°，

∴AE⊥BD，

∴AE＝BD且AE⊥BD．