Question

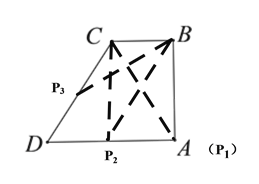
【题目】已知：如图，在四边形中ABCD中，AB⊥BC，AD∥BC，∠BCD=120°，BC=2，AD=DC.P为四边形ABCD边上的任意一点，当∠BPC=30°时，CP的长为______．

Answer 1

【答案】2或2 或4　

【解析】过点C作CE⊥AD， 连接AC，∵AD//BC，∠BCD=120°，∴∠D=180°-∠BCD=60°，∵AD=CD，∴△ACD是等边三角形，∴∠CAD=60°，AC=AD，∵∠BAD=90°，∴∠BAC=30°，即点P1与点A重合时，∠BP1C=30°，此时CP1=CA=4；

当点P2为AD中点时，此时四边形ABCP2是矩形，∴BP2=AC=4，∠BP2C=∠BCA=30°，∵∠BCP2=90°，∴CP2= =；

当点P3的CD边上时，∵∠BCD=120°，∠BCP3=30°，∴∠CBP3=30°，∴CP3=BC=2；

综上，当∠BPC=30°时，CP的长为4或或2.