题目内容
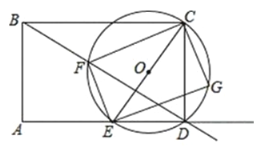
【题目】如图,矩形![]() 的边
的边![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 移动,以
移动,以![]() 为直径作圆
为直径作圆![]() ,点
,点![]() 为圆
为圆![]() 与射线
与射线![]() 的公共点,连接
的公共点,连接![]() ,过点
,过点![]() 作
作![]() ,
,![]() 与圆
与圆![]() 相交于点
相交于点![]() , 连接
, 连接![]() .
.
(1)试说明四边形![]() 是矩形;
是矩形;
(2)当圆![]() 与射线
与射线![]() 相切时,点
相切时,点![]() 停止移动,在点
停止移动,在点![]() 移动的过程中:
移动的过程中:
①矩形![]() 的面积是否存在最大值或最小值?若存在,求出这个最大值或最小值;若不存在,说明理由;
的面积是否存在最大值或最小值?若存在,求出这个最大值或最小值;若不存在,说明理由;
②求点![]() 移动路线的长.
移动路线的长.
【答案】(1)证明详见解析;(2)①最小值为![]() ;最大值为2
;最大值为2![]() ;②
;②![]() cm.
cm.
【解析】
试题(1)只要证得三个内角等于90°即可;
(2)①应用三角函数可得![]() ,所以
,所以![]() ,然后只需求出CF的范围就可以求出
,然后只需求出CF的范围就可以求出![]() 的范围;
的范围;
②根据圆周角定理和矩形的性质可证得∠GDC=∠FDE=定值,从而得到点G的移动的路线是线段,只需找到点G的起点和终点,求出该线段的长度即可.
试题解析:(1)∵CE是⊙O的直径,点F、G在⊙O上,∴∠EFC=∠EGC=90°,
又∵EG⊥EF,∴∠FEG=90°,∴四边形EFCG是矩形;
(2)①∵四边形EFCG是矩形,∴∠BCD=90°,∴![]() ,
,
∵∠CEF=∠BDC,∴![]() =
=![]() ,即
,即![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵当点F与点B重合时,CF=BC=4;
当⊙O与射线BD相切时,点F与点D重合,
此时CF=CD=3;
当CF⊥BD时,![]() ,
,
∴![]() ,
,
∴当CF=![]() cm时,
cm时,![]() 取得最小值为
取得最小值为![]() ,
,
当CF=4cm时,![]() 取得最大值为2
取得最大值为2![]() .
.
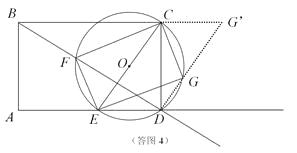
②如答图4,连接DG,并延长DG交BC得延长线与点G’.
∵∠BDG=∠FEG=90°,又∵∠DCG’=90°,∴点G得移动路线为线段DG’,
∵CD=3cm,∴CG’=![]() ,∴DG’=
,∴DG’=![]() (cm).
(cm).

练习册系列答案
相关题目