题目内容
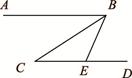
如图a是长方形纸带，∠DEF=25°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠DHF的度数是（ ）
| A．35° | B．50° | C．65° | D．75° |
D
解析试题分析：根据两条直线平行，内错角相等，则∠BFE=∠DEF=25°，根据平角定义，则∠EFC=155°，进一步求得∠BFC=155°-25°=130°，进而求得∠CFE=130°-25°=105°，再根据平行线的性质即可求解．
∵AD∥BC，∠DEF=25°，
∴∠BFE=∠DEF=25°，
∴∠EFC=155°，
∴图c中，∠BFC=155°-25°=130°，
∴∠CFE=130°-25°=105°，
∴∠DHF=75°．
故选：D．
考点：翻折变换（折叠问题）.
练习册系列答案
一线名师提优试卷系列答案
相关题目
如图，已知AB∥CD，则∠α、∠β和∠γ之间的关系为 ( )
| A．β＋γ－α＝180° | B．α＋γ＝β |
| C．α＋β＋γ＝360° | D．α＋β－2γ＝180° |
下列说法中正确的个数有( )
（1）在同一平面内，不相交的两条直线必平行．
（2）在同一平面内，不相交的两条线段必平行．
（3）相等的角是对顶角．
（4）两条直线被第三条直线所截，所得到同位角相等．
（5）两条平行线被第三条直线所截，一对内错角的角平分线互相平行．
| A．1个 | B．2个 | C．3个 | D．4个 |
如图，是我们学过的用直尺和三角尺画平行线的方法示意图，画图的原理是（ ）
| A．同位角相等，两直线平行 | B．内错角相等，两直线平行 |
| C．两直线平行，同位角相等 | D．两直线平行，内错角相等 |
，则∠BED 的度数是（ ）
如图,△ABC中，∠A=90°，点D在AC边上，DE∥BC，如果∠1=145°，那么∠B的度数为（ ）
A．35° | B．25° | C．45° | D．55° |
如图所示，如果AB∥CD，则∠1、∠2、∠3之间的关系为（ ）
| A．∠1+∠2+∠3=360° | B．∠1-∠2+∠3=180° |
| C．∠1+∠2-∠3-180° | D．∠1+∠2-∠3=180° |
如图，AB∥CD，CE平分∠BCD，∠DCE=18°，则∠B的度数为（ ）
| A．18° | B．36° | C．45° | D．54° |
如图，AB∥EF，∠C=90°，则α、β、γ的关系为（ ）
| A．β=α+γ | B．α+β+γ=180° | C．β+γ-α=90° | D．α+β-γ=90° |