题目内容
如图，已知AB∥CD，BC平分∠ABE，∠C=
，则∠BED 的度数是（ ）
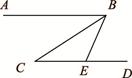
A． | B． | C． | D． |
D.
解析试题分析：由AB∥CD，根据两直线平行，内错角相等的性质，得∠ABC=∠C=33°；
由BC平分∠ABE得∠ABC=∠CBD=33°；
根据三角形的一外角等于与它不相邻的两内角之和，得∠BED=∠C+∠CBE=66°.
故选D.
考点：1.平行线的性质；2.三角形外角定理.
练习册系列答案
相关题目
如图所示，AB∥CD，点E在CB的延长线上．若∠ABE＝70°，则∠ECD的度数为（ ）
| A．20° | B．70° | C．100° | D．110° |
AB的长为半径画孤，两弧相交于点M，N，作直线MN，交BC于点D，连接AD．若△ADC的周长为10，AB=7，则△ABC的周长为（ ）。
如下图, AB∥CD, OE平分∠BOC, OF⊥OE, OP⊥CD, ∠ABO＝
a°, 则下列结论:
①∠BOE＝
(180-a)°；②OF平分∠BOD；③∠POE＝∠BOF；④∠POB＝2∠DOF．
其中正确的个数有多少个？ （ ）
| A．1 | B．2 | C．3 | D．4 |
如图，直线a，b被直线c所截，a∥b，∠1=∠2，若∠3=40°，则∠4等于（ ）
| A．40° | B．50° | C．70° | D．80° |
如图，AB∥CD，AD平分∠BAC，∠C=80°，则∠D的度数为( )。
| A．50° | B．55° | C．70° | D．80° |